题目内容
11. 如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于( )
如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于( )| A. | 180° | B. | 225° | C. | 270° | D. | 315° |
分析 首先判定△ABC≌△AEF,△ABD≌△AEH,可得∠5=∠BCA,∠4=∠BDA,然后可得∠1+∠5=∠1+∠BCA=90°,∠2+∠4=∠2+∠BDA=90°,然后可得∠1+∠2+∠3+∠4+∠5的值.
解答 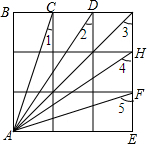 解:在△ABC和△AEF中,$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠E}\\{BC=EF}\end{array}\right.$,
解:在△ABC和△AEF中,$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠E}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△AEF(SAS),
∴∠5=∠BCA,
∴∠1+∠5=∠1+∠BCA=90°,
在△ABD和△AEH中,$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠E}\\{DB=HE}\end{array}\right.$,
∴△ABD≌△AEH(SAS),
∴∠4=∠BDA,
∴∠2+∠4=∠2+∠BDA=90°,
∵∠3=45°,
∴∠1+∠2+∠3+∠4+∠5=90°+90°+45°=225°.
故选:B.
点评 此题主要考查了全等三角形的判定和性质,关键是掌握全等三角形的性质:全等三角形对应角相等.

练习册系列答案
相关题目
1.已知反比例函数y=$\frac{k-1}{x}$的图象经过点(-2,3),下列各点不在其图象上的是( )
| A. | (-1,6) | B. | (3,-2) | C. | (5,-1) | D. | (4$\frac{1}{2}$,-1$\frac{1}{3}$) |
16. 如图,⊙O的直径AB=8,点C在⊙O上,∠ABC=30°,则AC的长是( )
如图,⊙O的直径AB=8,点C在⊙O上,∠ABC=30°,则AC的长是( )
 如图,⊙O的直径AB=8,点C在⊙O上,∠ABC=30°,则AC的长是( )
如图,⊙O的直径AB=8,点C在⊙O上,∠ABC=30°,则AC的长是( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4 |
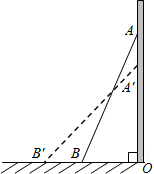 如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯多少米?
如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯多少米? 一张长方形纸如图,AB=12,AD=7.2,把它裁成两张长方形纸,使得其中一张和原纸相似,应怎样裁?有没有可能使两张纸都和原纸相似?
一张长方形纸如图,AB=12,AD=7.2,把它裁成两张长方形纸,使得其中一张和原纸相似,应怎样裁?有没有可能使两张纸都和原纸相似?