题目内容
1. 一张长方形纸如图,AB=12,AD=7.2,把它裁成两张长方形纸,使得其中一张和原纸相似,应怎样裁?有没有可能使两张纸都和原纸相似?
一张长方形纸如图,AB=12,AD=7.2,把它裁成两张长方形纸,使得其中一张和原纸相似,应怎样裁?有没有可能使两张纸都和原纸相似?
分析 根据相似多边形的性质求出CE的长,根据相似多边形的判定定理进行判断即可.
解答 解: 当四边形CEFB∽四边形DABC时,
当四边形CEFB∽四边形DABC时,
$\frac{CE}{BC}$=$\frac{BC}{AB}$,即$\frac{CE}{7.2}$=$\frac{7.2}{12}$,
解得,CE=4.32,
则DE=12-4.32=7.68,
$\frac{7.68}{7.2}$≠$\frac{7.2}{12}$,
∴没有可能使两张纸都和原纸相似.
点评 本题考查的是相似多边形的性质和判定,掌握相似多边形的性质为:对应角相等;对应边的比相等是解题的关键.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
11. 如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于( )
如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于( )
 如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于( )
如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于( )| A. | 180° | B. | 225° | C. | 270° | D. | 315° |
12.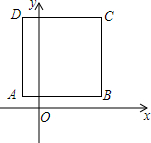 如图,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为( )
如图,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为( )
 如图,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为( )
如图,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为( )| A. | (3,1) | B. | (-1,1) | C. | (3,5) | D. | (-1,5) |
9.满足方程|x-2|+|x+1|=3的x的个数是( )
| A. | 多于2个 | B. | 2个 | C. | 1个 | D. | 0个 |
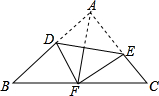 如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且EF=$\frac{1}{2}$AB;②∠BAF=∠CAF;③S四边形ADFE=$\frac{1}{2}$S△ABC;④∠BDF+∠FEC=2∠BAC,正确的是④(把你认为正确的都填上,成立的说明理由).
如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且EF=$\frac{1}{2}$AB;②∠BAF=∠CAF;③S四边形ADFE=$\frac{1}{2}$S△ABC;④∠BDF+∠FEC=2∠BAC,正确的是④(把你认为正确的都填上,成立的说明理由).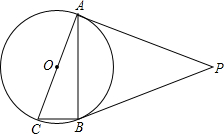 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.