题目内容
12.在Rt△ABC中,∠C=90°,sinA=$\frac{5}{13}$,则tanA的值为( )| A. | $\frac{12}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{13}{12}$ | D. | $\frac{12}{5}$ |
分析 根据三角函数的定义,sinA=$\frac{BC}{AB}$=$\frac{5}{13}$,因而可以设BC=5k,则AB=13k,根据勾股定理可以求得AC的长,然后利用正切的定义即可求解.
解答 解:∵在Rt△ABC中,∠C=90°,sinA=$\frac{BC}{AB}$=$\frac{5}{13}$,
∴设BC=5k,则AB=13k,
根据勾股定理可以得到:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=12k,
∴tanA=$\frac{BC}{AC}$=$\frac{5k}{12k}$=$\frac{5}{12}$.
故选B.
点评 本题考查了三角函数的定义,正确理解三角函数可以转化成直角三角形的边的比值,是解题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
3. 如图,线段DE是△ABC的中位线,∠B=60°,则∠ADE的度数为( )
如图,线段DE是△ABC的中位线,∠B=60°,则∠ADE的度数为( )
 如图,线段DE是△ABC的中位线,∠B=60°,则∠ADE的度数为( )
如图,线段DE是△ABC的中位线,∠B=60°,则∠ADE的度数为( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |
20.下列计算正确的个数是( )
①(x+y)2=x2+y2
②(-x+y)2=x2-2xy+y2
③(x+2y)(x-2y)=x2-2y2
④(-2a-3)(2a-3)=9-4a2
⑤(a-b)2=a2-b2.
①(x+y)2=x2+y2
②(-x+y)2=x2-2xy+y2
③(x+2y)(x-2y)=x2-2y2
④(-2a-3)(2a-3)=9-4a2
⑤(a-b)2=a2-b2.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
4.下列等式成立的是( )
| A. | (a+b)2=a2+b2 | B. | (a-b)2=a2-b2 | C. | (x-4)(x+4)=x2-4 | D. | (a+b)2=a2+b2+2ab |
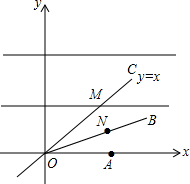 如图点A(2,0)点N在射线OB上运动,点M是直线y=x上一动点,OB为∠AOC的角平分线,求AN+MN的最小值,要画出图象.
如图点A(2,0)点N在射线OB上运动,点M是直线y=x上一动点,OB为∠AOC的角平分线,求AN+MN的最小值,要画出图象.