题目内容
2.已知$\frac{2x-5}{(x+1)(x-3)}=\frac{A}{x+1}+\frac{B}{x-3}$,求A,B的值.分析 已知等式右边通分并利用同分母分式的加法法则计算,利用分式相等的条件求出A与B的值即可.
解答 解:$\frac{2x-5}{(x+1)(x-3)}$=$\frac{A}{x+1}$+$\frac{B}{x-3}$=$\frac{(A+B)x+B-3A}{(x+1)(x-3)}$,
可得:2x-5=(A+B)x+B-3A,即$\left\{\begin{array}{l}{A+B=2}\\{B-3A=-5}\end{array}\right.$,
解得:A=$\frac{7}{4}$,B=$\frac{1}{4}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12.一个多边形的内角和是外角和的3倍,则这个多边形是( )
| A. | 六边形 | B. | 七边形 | C. | 八边形 | D. | 九边形 |
13.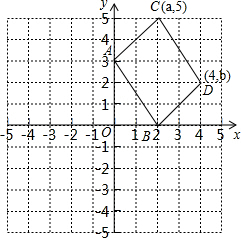 如图,平移线段AB得到线段CD,已知:A(0,3),B(2,0),C(a,5),D(4,b).
如图,平移线段AB得到线段CD,已知:A(0,3),B(2,0),C(a,5),D(4,b).
(1)将线段AB向右平移2个单位,再向上平移2个单位得到线段CD;
(2)四边形ABDC的面积是15.
 如图,平移线段AB得到线段CD,已知:A(0,3),B(2,0),C(a,5),D(4,b).
如图,平移线段AB得到线段CD,已知:A(0,3),B(2,0),C(a,5),D(4,b).(1)将线段AB向右平移2个单位,再向上平移2个单位得到线段CD;
(2)四边形ABDC的面积是15.
10.某次数学考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我组成绩是87分的同学最多.”小英说:“我们组的7位同学成绩排在最中间的恰好也是87分.”上面两位同学的话能反映的统计量是( )
| A. | 众数和平均数 | B. | 平均数和中位数 | C. | 众数和方差 | D. | 众数和中位数 |
11.直线y=x-2不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.在Rt△ABC中,∠C=90°,sinA=$\frac{5}{13}$,则tanA的值为( )
| A. | $\frac{12}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{13}{12}$ | D. | $\frac{12}{5}$ |
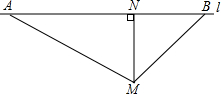 如图,根据道路管理规定,在某笔直的大道AB上行驶的车辆,限速60千米/时,已知测速站点M距大道AB的距离MN为30米,现有一辆汽车从A向B方向匀速行驶,测得此车从A点行驶到B点所用时间危机6秒,∠AMN=60°,∠BMN=45°.
如图,根据道路管理规定,在某笔直的大道AB上行驶的车辆,限速60千米/时,已知测速站点M距大道AB的距离MN为30米,现有一辆汽车从A向B方向匀速行驶,测得此车从A点行驶到B点所用时间危机6秒,∠AMN=60°,∠BMN=45°.