题目内容
10.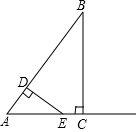 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点D从点A出发以每秒3个单位的速度运动至点B,过点D作DE⊥AB交射线AC于点E.设点D的运动时间为t秒(t>0).
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点D从点A出发以每秒3个单位的速度运动至点B,过点D作DE⊥AB交射线AC于点E.设点D的运动时间为t秒(t>0).(1)线段AE的长为5t.(用含t的代数式表示)
(2)若△ADE与△ACB的面积比为1:4时,求t的值.
(3)设△ADE与△ACB重叠部分图形的周长为L,求L与t之间的函数关系式.
(4)当直线DE把△ACB分成的两部分图形中有一个是轴对称图形时,直接写出t的值.
分析 (1)先在Rt△ABC中求出tanA,再在Rt△ADE中求出DE,最后用勾股定理即可得出结论;
(2)方法一:先判断出△ABC∽△AED,进而得出DE=4t,再用三角形的面积公式得出△ADE,△ABC的面积,用面积比建立方程即可得出结论;
方法二、先判断出△ABC∽△AED,再用$\frac{{{S_{△ADE}}}}{{{S_{△AC{B_{\;}}}}}}=\frac{1}{4}$,得出$\frac{AD}{AC}=\frac{1}{2}$.而AC=3,AD=3t,即可得出结论;
(3)分两种情况讨论计算,都是四边形是轴对称图形,用相等的线段建立方程求解即可.
解答 解:(1)在Rt△ABC中,tanA=$\frac{BC}{AC}$=$\frac{4}{3}$
由题意得,AD=3t,
在Rt△ADE中,tanA=$\frac{DE}{AD}$=$\frac{DE}{3t}$=$\frac{4}{3}$,
根据勾股定理得,AE=5t.
故答案为5t;
(2)方法一:∵ED⊥AB,
∴∠ADE=90°.∵∠ACB=90°,
∴∠ACB=∠ADE.∠A=∠A,
∴△ABC∽△AED,
∴$\frac{AD}{AC}=\frac{DE}{BC}$.
∵AD=3t,AC=3,BC=4,
∴DE=4t.
∴${S_{△ADE}}=\frac{1}{2}×3t×4t=6{t^2}$.
∵${S_{△ACB}}=\frac{1}{2}×3×4=6$,
∵$\frac{{{S_{△ADE}}}}{{{S_{△AC{B_{\;}}}}}}=\frac{1}{4}$,
∴$6{t^2}=\frac{1}{4}×6$.
∴${t_1}=\frac{1}{2},{t_2}=-\frac{1}{2}$(舍)
∴t的值为$\frac{1}{2}$.
方法二:∵ED⊥AB,
∴∠ADE=90°.
∵∠ACB=90°,
∴∠ACB=∠ADE.
∵∠A=∠A,
∴△ABC∽△AED,
∵$\frac{{{S_{△ADE}}}}{{{S_{△AC{B_{\;}}}}}}=\frac{1}{4}$,
∴$\frac{AD}{AC}=\frac{1}{2}$.
∵AC=3,AD=3t,
∴2×3t=3,t=$\frac{1}{2}$.
(3)由(2)得:△ABC∽△AED,
∴$\frac{AC}{AD}=\frac{BC}{DE}=\frac{AB}{AE}$.
∵AD=3t,
∴DE=4t,AE=5t.BD=5-3t,
∴当$0<t≤\frac{3}{5}$时,L=3t+4t+5t=12t.
∴L=12t.
当$\frac{3}{5}<t≤\frac{5}{3}$时,如图,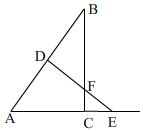
∵∠B=∠B,∠BDF=∠BCA,
∴△ABC∽△FBD,
∴$\frac{BD}{BC}=\frac{DF}{AC}$.
∵BD=5-3t,
∴$DF=\frac{15}{4}-\frac{9}{4}t$.
∵∠BFD=∠EFC,∠BDF=∠ECF,
∴∠B=∠E,
∵∠FCE=∠BCA
∴△BCA∽△ECF,
∴$\frac{CF}{AC}=\frac{CE}{BC}$.
∵CE=5t-3,
∴$CF=\frac{15}{4}t-\frac{9}{4}$.
$L=3t+3+\frac{15}{4}t-\frac{9}{4}+\frac{15}{4}-\frac{9}{4}t=\frac{9}{2}t+\frac{9}{2}$.
∴$L=\frac{9}{2}t+\frac{9}{2}$.
(4)由(1)知,AE=5t,DE=4t,
∴CE=3-5t,
当DE=CE时,四边形BCED是轴对称图形,
∴4t=3-5t,
∴t=$\frac{1}{3}$,
当DE和BC相交于F,AD=AC时,四边形ACFE是轴对称图形,
∵AD=3t,AC=3,
∴3t=3,
∴t=1.
即:满足条件的时间t为$\frac{1}{3}$或1.
点评 此题是几何变换综合题,主要考查了直角三角形的性质,锐角三角函数,轴对称图形,勾股定理,相似三角形的性质和判定,判断△ABC∽△AED,是解本题,得到L的函数关系式是解本题的难点.

| 星 期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌(元) | +4 | +4.5 | -1 | -2.5 | +2 |
(2)本周内的最高价每股是多少元?最低价每股是多少元?
(3)已知李丽买进股票时付1.5‰的手续费,卖出时需付1.5‰成交费的手续费和1‰的交易费,如果她在星期六收盘时全部卖出,她的收益情况如何?
| 销售量(万件) | 平均每件产品的利润(元) | |
| 网上销售 | x | 当0<x≤2时,y1=140 |
| 当2≤x<6时,y1=-5x+150 | ||
| 批发部销售 | n | 当0<n≤2时,y2=120 |
| 当2≤n<6时,y2=-5n+130 |
②y2与x的函数关系为:当0<x≤4时,y2=5x+100;当4≤x<6时,y2=120.
(2)求每年该公司销售这种花卉产品的总利润w(万元)与网上销售数量x(万件)的函数关系式,并指出x的取值范围;
(3)该公司每年网上、批发部的销售量各为多少万件时,可使公司每年的总利润最大?最大值为多少万元?

 如图,已知抛物线y=x2+bx+c与一直线相交于A(-1,0),C(2,-3)两点,与y轴交于点N,其顶点为D.
如图,已知抛物线y=x2+bx+c与一直线相交于A(-1,0),C(2,-3)两点,与y轴交于点N,其顶点为D.