题目内容
18.a是一个给定的整数,当a为何值时,关于x和y的方程y3+1=a(xy-1)有正整数解?在有正整数解时,求解该不定方程.分析 先判断出xy-1|y3+1,当且仅当xy-1|x3+1,然后分情况讨论计算,取特殊数计算即可.
解答 解:若有质数p|x3、p|xy-1,则p|x,从而p|1,矛盾.所以(x3,xy-1)=1.所以xy-1|y3+1,当且仅当xy-1|x3(y3+1).
因为x3(y3+1)=(x3y3-1)+(x3+1),显然xy-1|x3y3-1,
所以xy-1|y3+1,当且仅当xy-1|x3+1.
(1)若y=1,2=a(x-1),所以x=2或x=3,a=2或1.
(2)类似地,若x=1,则y3+1=a(y-1).所以y=2或y=3,a=9或a=14.
(3)由于有条件,不妨设.
若x=y,则x3+1=a(x2-1),所以x=y=2,a=3.
若x>y,则y3>a(y2-1),
因为a,y为整数,所以y=2或y=3.
当y=2时,x=5;当y=3时,x=5.对应的a为1或2.
由条件知x=2,y=5;以及x=3,y=5也是原方程的解,对应的整数a是14或9.
综上,当a=1、2、3、9、14时,原不定方程有正整数解,它们分别是:(3,1),(5,2);(2,1),(5,3);(2,2);(1,2),(3,5);(1,3),(2,5).
点评 此题是一次不定方程(组),主要考查有理数整数解,解本题的关键是xy-1|y3+1,当且仅当xy-1|x3+1.

练习册系列答案
相关题目
3.下列运算中正确的是( )
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B. | 2$\sqrt{3}$+3$\sqrt{3}$=6$\sqrt{3}$ | C. | $\sqrt{6}$$÷\sqrt{2}$=$\sqrt{3}$ | D. | ($\sqrt{2}$+1)($\sqrt{2}$-1)=3 |
7.使一元二次方程x2+3x+m=0有整数根的非负整数m的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
1.下列方程的变形中,正确的是( )
| A. | 若y-4=8,则y=8-4 | |
| B. | 若2(2x-3)=2,则4x-6=2 | |
| C. | 若-$\frac{1}{2}$x=4,则x=-2 | |
| D. | 若 $\frac{1}{3}$-$\frac{t-1}{2}$=1,则去分母得2-3(t-1)=1 |
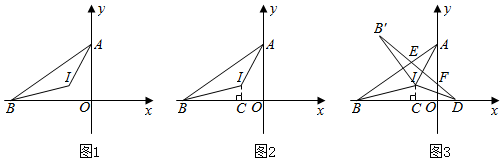
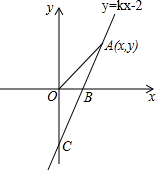 如图,直线y=kx-2与x轴,y轴分别交于B,C两点,其中OB=1.
如图,直线y=kx-2与x轴,y轴分别交于B,C两点,其中OB=1.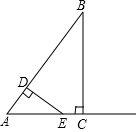 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点D从点A出发以每秒3个单位的速度运动至点B,过点D作DE⊥AB交射线AC于点E.设点D的运动时间为t秒(t>0).
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点D从点A出发以每秒3个单位的速度运动至点B,过点D作DE⊥AB交射线AC于点E.设点D的运动时间为t秒(t>0).