题目内容
3.甲、乙、丙三个班的学生要到离学校21干米的某校参观,学校只有一辆车,只能坐一个班的学生,汽车的速度是36千米/时,学生步行的速度是4干米/时,要使三个班的学生同时到达目的地,最少需要多少小时?分析 要想一同到达就必须停车两次,设第一次停车到第二次停车学生步行了x千米,第二次停车到第三次停车学生步行了y千米,则第一次停车时走了(21-x-y)千米,根据时间相等可得关于x、y的方程,据此即可解答问题.
解答 解:设第一次停车到第二次停车学生步行了x千米,第二次停车到第三次停车学生步行了y千米,则第一次停车时走了(21-x-y)千米,则
第一次停车的所用的时间:$\frac{x}{4}$=$\frac{21-x-y+21-y}{36}$,
化简得9x=42-x-2y
第二次停车的所用的时间:$\frac{y}{4}$=$\frac{21-y+21}{36}$,
解得:y=4.2,
代入方程9x=42-x-2y得:x=3.36,
所以时间$\frac{4.2}{4}$+$\frac{3.36}{4}$=1.89(小时).
答:要使三个班的学生同时到达目的地,最少需要1.89小时.
点评 此题主要考查了二元一次方程组的应用,应抓住甲乙丙三个班坐车行驶的时间、路程以及他们各自间的距离关系是解题关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
16.若$\frac{1}{2}$m+1与m-2互为相反数,则m的值为( )
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
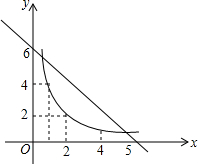 已知矩形A的长、宽分别是2和1,是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?
已知矩形A的长、宽分别是2和1,是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?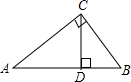 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,互余的角是∠A与∠B、∠ACD与∠BCD、∠A与∠ACD、∠B与∠BCD;互补的角是∠ADC与∠BDC、∠ADC与∠ACB、∠ACB与∠BDC.
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,互余的角是∠A与∠B、∠ACD与∠BCD、∠A与∠ACD、∠B与∠BCD;互补的角是∠ADC与∠BDC、∠ADC与∠ACB、∠ACB与∠BDC.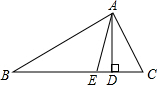 在△ABC中,∠BAC=90°,AC=5cm,AD是高,AE是斜边上的中线,且DC=$\frac{1}{2}$AC,求∠B的度数及AE的长.
在△ABC中,∠BAC=90°,AC=5cm,AD是高,AE是斜边上的中线,且DC=$\frac{1}{2}$AC,求∠B的度数及AE的长.