题目内容
19.如图1,等边△ABC中,D是AB上一点,以CD为边向上作等边△CDE,连结AE.(1)求证:AE∥BC;
(2)如图2,若点D在AB的延长线上,其余条件均不变,(1)中结论是否成立?请说明理由.
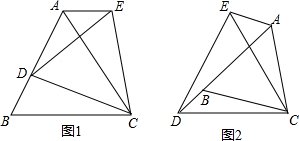
分析 (1)根据已知条件先证出∠BCD=∠ACE,再根据SAS证出△DBC≌△ACE,得出∠B=∠CAE=∠BAC=60°,从而得出∠B+∠BAE=180,再根据平行线的判定即可证出AE∥BC;
(2)根据(1)证出的△DBC≌△ACE,得出∠BDC=∠AEC,在△DMC和△AME中,根据AA证出△DMC∽△AME,得出∠EAM=∠DCM=60°,再根据∠DCA+∠CAE=∠DCE+∠ECA+CEA=180°+∠ECA,即可得出AE∥BC.
解答 证明:(1)∵∠BCA=∠DCE=60°,
∴∠BCA-∠ACD=∠DCE-∠ACD,
即∠BCD=∠ACE,
∵△ABC和△DCE是等边三角形,
∴BC=AC,DC=EC,
在△BDC与△ACE中,
$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{DC=EC}\end{array}\right.$,
∴△DBC≌△ACE(SAS),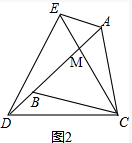
∴∠B=∠CAE,
∴∠B=∠CAE=∠BAC=60°,
∴∠CAE+∠BAC=∠BAE=120°,
∴∠B+∠BAE=180,
∴AE∥BC;
(2)成立,证明如下:
∵△DBC≌△ACE,
∴∠BDC=∠AEC,
在△DMC和△AME中,
∵∠BDC=∠AEC(已证),
∴∠DMC=∠EMA,
∴△DMC∽△EMA,
∴∠EAM=∠DCM=60°,
∴∠EAC=120°,
又∵∠DCA+∠CAE=∠DCE+∠ECA+CEA=180°+∠ECA,
∴AE∥BC.
点评 本题主要考查等边三角形的性质和全等三角形的判定与性质的知识点,解答本题的关键是能证出∠B=∠CAE=∠BAC,熟练掌握三角形全等的判定与性质定理.

练习册系列答案
相关题目
9.下列计算正确的是( )
| A. | -8-3=-5 | B. | $(-\frac{1}{3})×3÷3×(-\frac{1}{3})=1$ | C. | 7a+a=7a2 | D. | 4xy2-2xy2=2xy2 |
11.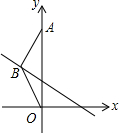 如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=-$\frac{1}{2}$x+1上,△ABO的面积是( )
如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=-$\frac{1}{2}$x+1上,△ABO的面积是( )
 如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=-$\frac{1}{2}$x+1上,△ABO的面积是( )
如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=-$\frac{1}{2}$x+1上,△ABO的面积是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
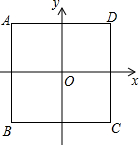 如图,正方形ABCD的边长为4,过它的中心建立平面直角坐标系(中心在原点上),各边和坐标轴平行或垂直.
如图,正方形ABCD的边长为4,过它的中心建立平面直角坐标系(中心在原点上),各边和坐标轴平行或垂直.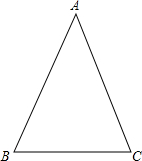 已知等腰△ABC,AB=AC=5,BC=4,请建立适当的平面直角坐标系,并求出A、B、C三点坐标.
已知等腰△ABC,AB=AC=5,BC=4,请建立适当的平面直角坐标系,并求出A、B、C三点坐标.