题目内容
4．若a1=1-$\frac{1}{m}$，a2=1-$\frac{1}{{a}_{1}}$，a3=1-$\frac{1}{{a}_{2}}$，则a2015的值为（ ）| A． | 1-$\frac{1}{m}$ | B． | -$\frac{1}{m-1}$ | C． | m | D． | $\frac{1}{m}$ |
分析 根据题意确定出a1，a2，a3，依此类推得出规律，即可确定出a2015的值．
解答 解：a1=1-$\frac{1}{m}$，a2=1-$\frac{1}{{a}_{1}}$=1-$\frac{1}{1-\frac{1}{m}}$=1-$\frac{m}{m-1}$=-$\frac{1}{m-1}$，a3=1-$\frac{1}{{a}_{2}}$=1+$\frac{1}{\frac{1}{m-1}}$=m，a4=1-$\frac{1}{m}$，
依此类推，
∵2015÷3=671…2，
∴a2015的值为-$\frac{1}{m-1}$，
故选B
点评 此题考查了分式的混合运算，弄清题中的规律是解本题的关键．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
相邻的两个整数是（ ）
12．
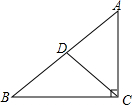如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD=5，AC=6，则tan∠DCB的值是（ ）
如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD=5，AC=6，则tan∠DCB的值是（ ）| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{4}{3}$ | D． | $\frac{3}{4}$ |
如图是大型输气管的截面图（圆形），某次数学实践活动中，数学课题学习小组为了计算大型输气管的直径，在圆形弧上取了A，B两点并连接AB，在劣弧AB上取中点C连接CB，经测量$BC=\frac{5}{4}$米，∠ABC=36.87°，请根据这些数据计算出大型输气管的直径（精确到0.1米）．（sin36.87°≈0.60，cos36.87°≈0.80，tan36.87°≈0.75）
9．
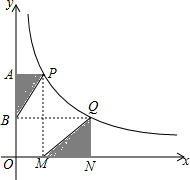如图，点P、Q是反比例函数y=$\frac{k}{x}$（k≠0）图象上的两点，PA⊥y轴于点A，QN⊥x轴于点N，作PM⊥x轴于点M，QB⊥y轴于点B，连接PB、QM，记S△ABP=S1，S△QMN=S2，则S1与S2的大小关系为（ ）
如图，点P、Q是反比例函数y=$\frac{k}{x}$（k≠0）图象上的两点，PA⊥y轴于点A，QN⊥x轴于点N，作PM⊥x轴于点M，QB⊥y轴于点B，连接PB、QM，记S△ABP=S1，S△QMN=S2，则S1与S2的大小关系为（ ）| A． | S1＞S2 | B． | S1＜S2 | C． | S1=S2 | D． | 无法判定 |
16．二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
下列结论：其中正确的序号为（1）、（3）、（4）．．
（1）ac＜0；
（2）当x＞1时，y的值随x值的增大而减小；
（3）3是方程ax2+（b-1）x+c=0的一个根；
（4）当-1＜x＜3时，ax2+（b-1）x+c＞0．
| X | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
（1）ac＜0；
（2）当x＞1时，y的值随x值的增大而减小；
（3）3是方程ax2+（b-1）x+c=0的一个根；
（4）当-1＜x＜3时，ax2+（b-1）x+c＞0．
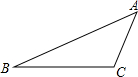如图，在△ABC中，∠ACB=120°，BC=2AC．