题目内容
11.三元一次方程组$\left\{\begin{array}{l}x+y=1\\ y+z=2\\ x+z=3\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=2}\end{array}\right.$.分析 方程组三个方程相加求出x+y+z的值,将每个方程代入即可求出x,y,z的值.
解答 解:$\left\{\begin{array}{l}{x+y=1①}\\{y+z=2②}\\{x+z=3③}\end{array}\right.$,
①+②+③得:2(x+y+z)=6,即x+y+z=3④,
把①代入④得:z=2,
把②代入④得:x=1,
把③代入④得:y=0,
则方程组的解为$\left\{\begin{array}{l}x=1\\ y=0\\ z=2\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=2}\end{array}\right.$
点评 此题考查了解三元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
1.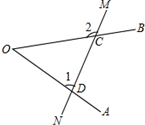 如图,直线MN和∠AOB的两边分别相交于点C,D.已知∠O=40°,∠2=125°,则∠1=( )
如图,直线MN和∠AOB的两边分别相交于点C,D.已知∠O=40°,∠2=125°,则∠1=( )
 如图,直线MN和∠AOB的两边分别相交于点C,D.已知∠O=40°,∠2=125°,则∠1=( )
如图,直线MN和∠AOB的两边分别相交于点C,D.已知∠O=40°,∠2=125°,则∠1=( )| A. | 85° | B. | 75° | C. | 65° | D. | 55° |
20. 如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )
如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )
 如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )
如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
1.某班一个小组7名同学的体育测试成绩(满分30分)依次为:27,29,27,25,27,30,25,这组数据的中位数和众数分别是( )
| A. | 27,25 | B. | 25,27 | C. | 27,27 | D. | 27,30 |
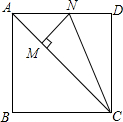 如图,已知正方形ABCD中,CM=CD,MN⊥AC,连接CN,则∠MNC=67.5°.
如图,已知正方形ABCD中,CM=CD,MN⊥AC,连接CN,则∠MNC=67.5°.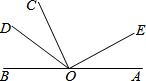 如图∠AOB是平角,过点O作射线OE,OC,OD.把∠BOE用图中的角表示成两个角或三个角和的形式,能有几种不同的表示方法( )
如图∠AOB是平角,过点O作射线OE,OC,OD.把∠BOE用图中的角表示成两个角或三个角和的形式,能有几种不同的表示方法( )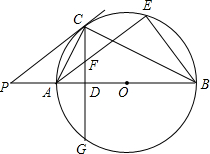 如图,AB为⊙O的直径,P是BA延长线一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.
如图,AB为⊙O的直径,P是BA延长线一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.