题目内容
3.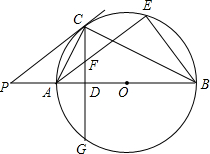 如图,AB为⊙O的直径,P是BA延长线一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.
如图,AB为⊙O的直径,P是BA延长线一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.(1)求证:△ACD∽△ABC;
(2)求证:∠PCA=∠ABC;
(3)过点A作AE∥PC交⊙O于点F,连接BE,若sin∠P=$\frac{3}{5}$,CF=5,求BE的长.
分析 (1)欲证明△ACD∽△ABC,只要证明①∠ADC=∠ACB,②∠CAD=∠BAC即可.
(2)利用等角的余角相等证明,即证明∠PCA+∠OCA=90°以及∠ABC+∠OAC=90°由此可以解决问题.
(3)先证明FA=FC=5,在RT△ADF中,根据sin∠FAD=$\frac{3}{5}$求出DF、AD,在RT△COD中利用勾股定理求出半径,最后在RT△ABE中利用sin∠BAE=$\frac{3}{5}$求出BE即可.
解答 (1)证明:∵AB是直径,
∴∠ACB=90°,
∵CG⊥AB,
∴∠ADC=90°=∠ACB,
∵∠CAD=∠BAC,
∴△ACD∽△ABC.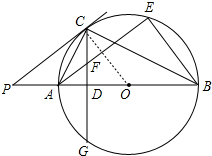
(2)证明:连接OC.
∵PC切⊙O于C,
∴OC⊥PC,
∴∠PCO=90°
∴∠PCA+∠OCA=90°,
∵∠ACB=90°,
∴∠ABC+∠OAC=90°,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠PCA=∠ABC.
(3)解:∵AE∥PC,
∴∠PCA=∠CAF,
∵AB⊥CG,
∴$\widehat{AC}$=$\widehat{AG}$,
∴∠ACF=∠ABC,
∵∠PCA=∠ABC,
∴∠ACF=∠CAF,
∴FA=FC,
∵CF=5,
∴AF=5,
∵AE∥PC,
∴∠FAD=∠P,
∵sin∠P=$\frac{3}{5}$,
∴sin∠FAD=$\frac{3}{5}$,
∴FD=3,AD=4,CD=8,
在RT△COD中,设CO=r,则有r2=(r-4)2+82
∴r=10,
∴AB=2r=20,
∵AB是直径,
∴∠AEB=90°,
∴sin∠EAB=$\frac{3}{5}$,
∴$\frac{EB}{AB}=\frac{3}{5}$,
∴$\frac{EB}{20}$=$\frac{3}{5}$,
∴EB=12.
点评 本题考查圆的有关知识、相似三角形的判定和性质、三角函数、勾股定理等知识,注意连接OC是圆中常用辅助线,熟练掌握垂径定理、切线的性质是解题的关键,属于中考压轴题.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案| A. | m2+n2=(m+n)(m-n) | B. | x2+2x-1=(x-1)2 | C. | a2-a=a(a-1) | D. | a2+2a+1=a(a+2)+1 |
| A. | $\sqrt{25}$=5 | B. | ±$\sqrt{64}$=±8 | C. | $\sqrt{(-6)^{2}}$=-6 | D. | $\root{3}{-8}$=-2 |
| A. | -7 | B. | 7 | C. | -13 | D. | 13 |
 如图,O是直线AB上的一点,射线OC,OE分别平分∠AOD和∠BOD.
如图,O是直线AB上的一点,射线OC,OE分别平分∠AOD和∠BOD.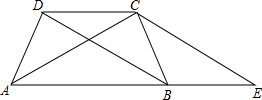 已知:如图,梯形ABCD中,DC∥AB,AD=BC=DC,AC、BD是对角线,E是AB延长线上一点,且∠BCE=∠ACD,联结CE.
已知:如图,梯形ABCD中,DC∥AB,AD=BC=DC,AC、BD是对角线,E是AB延长线上一点,且∠BCE=∠ACD,联结CE. 已知:如图,在直角梯形纸片ABCD中,DC∥AB,AB>CD>AD,∠A=90°,将纸片沿过点D的直线翻折,使点A落在边CD上的点E处,折痕为DF,联结EF并展开纸片.
已知:如图,在直角梯形纸片ABCD中,DC∥AB,AB>CD>AD,∠A=90°,将纸片沿过点D的直线翻折,使点A落在边CD上的点E处,折痕为DF,联结EF并展开纸片.