题目内容

14．已知，如图，M是等腰三角形ABC底边BC上的中点，DM⊥AB，EF⊥AB，ME⊥AC，DG⊥AC，求证：四边形MEND是菱形．

分析 首先证明EF∥DM，DG∥ME，可得四边形DNEM是平行四边形，再根据等腰三角形三线合一的性质可得DM=ME，进而可得四边形MEND是菱形．

解答 证明：连接AM，
∵DM⊥AB，EF⊥AB，ME⊥AC，DG⊥AC，
∴EF∥DM，DG∥ME，
∴四边形DNEM是平行四边形，
∵M是等腰三角形ABC底边BC上的中点，
∴AM是∠BAC的角平分线，
∴DM=ME，
∴四边形MEND是菱形．

点评 此题主要考查了菱形的判定，以及等腰三角形的性质，关键是掌握一组邻边相等的平行四边形是菱形．

练习册系列答案
相关题目
18．下列命题中真命题是（　　）
A．位似图形一定是相似形B．相似形一定是位似图形
C．两个直角三角形是相似三角形D．两个直角三角形是位似三角形
19．解方程：5x2-3$\sqrt{5}$x+2=0．
2．如图1，在平面直角坐标系中，正方形OABC的顶点A和C分别在x轴和y轴正半轴上，点B坐标为（3，3），抛物线y=-x2+bx+c过点A、C，交x轴负半轴于点D，与BC边的另一个交点为E，抛物线的顶点为M，对称轴交x轴于点N．
（1）求抛物线的函数关系式；
（2）点P在直线MN上，求当PE+PA的值最小时点P的坐标；
（3）如图2，探索在x轴是否存在一点F，使∠CFO=∠CDO-∠CAO？若存在，求点F的坐标；不存在，说明理由；
（4）将抛物线沿y轴方向平移m个单位后，顶点为Q，若QO平分∠CQN，求点Q的坐标．
9．在平面直角坐标系中，抛物线y=ax2+bx+3与x轴的两个交点分别为A（-3，0）、B（1，0），过顶点C作CH⊥x轴于点H．
（1）求抛物线的解析式和顶点C的坐标．
（2）在y轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标．
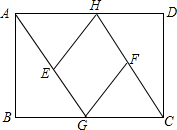19．如图，在矩形ABCD中，H是AD上任意一点，AG∥CH交BC于点G，点E、F分别为AG、CH的中点，连接HE、FG．
（1）求证：四边形HEGF是平行四边形；
（2）当点G是BC的中点时，求证：四边形HEGF是菱形．
6．已知，如图，AB∥CD，EF分别交AB、CD于点E、F，EG平分∠AEF，FH平分∠EFD，求证：EG∥FH．
3．如图，D是△ABC的BC边上的点，BD：DC=2：1，点E是AD的中点，连接BE并延长交AC于点F，求BE：EF的值．
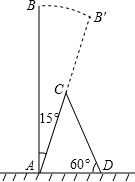4．一棵大树树干AB（假定树干AB垂直于地面）被刮倾斜15°后折断在地上，树的项部恰好接触到地面D（如图所示），量得树干的倾斜角为∠BAC=15°，大树被折断部分和地面所成的角∠ADC=60°，AD=3.6米，求这棵大树AB原来的高度是多少米？（参考数据：$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7，$\sqrt{6}$≈2.4）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网