题目内容
7. 如图,AB∥DE,△ACB是等腰直角三角形,且∠C=90°,CB的延长线交DE于点G,则∠CGE=135度.
如图,AB∥DE,△ACB是等腰直角三角形,且∠C=90°,CB的延长线交DE于点G,则∠CGE=135度.
分析 先根据等腰直角三角形的性质求出∠ABC的度数,再由平行线的性质求出∠DGB的度数,根据补角的定义即可得出结论.
解答 解:∵△ACB是等腰直角三角形,且∠C=90°,
∴∠ABC=45°.
∵AB∥DE,
∴∠DGB=∠ABC=45°,
∴∠CGE=180°-45°=135°.
故答案为:135.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
相关题目
18. 如图,经过平移能得到如图图形的是( )
如图,经过平移能得到如图图形的是( )
 如图,经过平移能得到如图图形的是( )
如图,经过平移能得到如图图形的是( )| A. |  | B. |  | C. |  | D. |  |
2.下列运算中,结果是a6的是( )
| A. | a3•a2 | B. | (a3)3 | C. | a3+a3 | D. | (-a)6 |
12.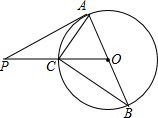 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )
 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )| A. | 3$\sqrt{3}$ | B. | 4 | C. | 5 | D. | 6 |
19.下列运算正确的是( )
| A. | a+a=2a2 | B. | a2•a=2a2 | C. | (-ab)2=2ab2 | D. | (2a)2÷a=4a |
16.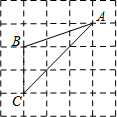 如图,△ABC的三个顶点均在格点上,则cosA的值为( )
如图,△ABC的三个顶点均在格点上,则cosA的值为( )
 如图,△ABC的三个顶点均在格点上,则cosA的值为( )
如图,△ABC的三个顶点均在格点上,则cosA的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | 2 | D. | $\frac{2\sqrt{5}}{5}$ |
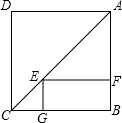 如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E、F.若正方形ABCD的周长是40cm,
如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E、F.若正方形ABCD的周长是40cm,