题目内容
17.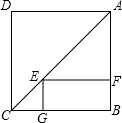 如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E、F.若正方形ABCD的周长是40cm,
如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E、F.若正方形ABCD的周长是40cm,(1)证明四边形BFEG是矩形;
(2)求四边形EFBG的周长.
分析 (1)根据三个角是直角的四边形是矩形进行判断即可.
(2)只要证明四边形EFBG的周长=AB+BC即可.
解答 (1)证明:∵四边形ABCD是正方形,AC是对角线
∴∠B=90°,∠BCA=∠BAC=45°
∵EF⊥AB,EG⊥BC.
∴∠EGB=∠EFB=90°,
∴四边形BFEG是矩形
(2)解:∵四边形BFEG是矩形
∴EG=BF,EF=BG,
∴∠CEG=∠ECG=45°,∠AEF=∠FAE=45°,
∴△CEG,△AEF都是等腰直角三角形.
即EG=CG AF=EF.
∵正方形ABCD的周长是40cm,
∴AB=BC=AD=CD=10cm,
∴矩形BFEG周长=BG+EG+BF+EF=BC+AB=10+10=20(cm).
点评 本题考查正方形的性质、矩形的判定和性质等知识,解题的关键是熟练掌握这些知识,属于基础题,中考常考题型.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
2.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (ab)2=ab2 | C. | 2a4×3a5=6a9 | D. | (a2)3=a5 |
9.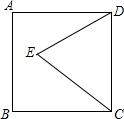 如图,正方形ABCD的边长为6,以CD为一边作等边三角形△DCE,点E在正方形内部,则点E到CD的距离是( )
如图,正方形ABCD的边长为6,以CD为一边作等边三角形△DCE,点E在正方形内部,则点E到CD的距离是( )
 如图,正方形ABCD的边长为6,以CD为一边作等边三角形△DCE,点E在正方形内部,则点E到CD的距离是( )
如图,正方形ABCD的边长为6,以CD为一边作等边三角形△DCE,点E在正方形内部,则点E到CD的距离是( )| A. | 6 | B. | 3$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
6.下列运算正确的是( )
| A. | (ab)3=a3b | B. | (a+b)2=a2+b2 | C. | a6÷a2=a3 | D. | π0=1 |
 如图,在△ABC中,AB=BC=12cm,∠ABC=80°,BE是∠ABC的平分线,DE∥BC.
如图,在△ABC中,AB=BC=12cm,∠ABC=80°,BE是∠ABC的平分线,DE∥BC. 如图,AB∥DE,△ACB是等腰直角三角形,且∠C=90°,CB的延长线交DE于点G,则∠CGE=135度.
如图,AB∥DE,△ACB是等腰直角三角形,且∠C=90°,CB的延长线交DE于点G,则∠CGE=135度.