题目内容
18.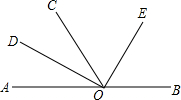 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC.
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC.(1)填空:∠BOD=155度;
(2)当∠DOE=90°,请说明OE平分∠BOC.
分析 (1)根据∠BOD=∠DOC+∠BOC,首先利用角平分线的定义和邻补角的定义求得∠DOC和∠BOC即可;
(2)根据∠COE=∠DOE-∠DOC和∠BOE=∠BOD-∠DOE分别求得∠COE与∠BOE的度数即可说明.
解答 解:(1)∵∠AOC=50°,OD平分∠AOC,
∴∠DOC=$\frac{1}{2}$∠AOC=25°,∠BOC=180°-∠AOC=130°,
∴∠BOD=∠DOC+∠BOC=155°;
(2)∵∠DOE=90°,∠DOC=25°,
∴∠COE=∠DOE-∠DOC=90°-25°=65°.
又∵∠BOE=∠BOD-∠DOE=155°-90°=65°,
∴∠COE=∠BOE,
∴OE平分∠BOC.
故答案为:155.
点评 本题主要考查了角的度数的计算,正确理解角平分线的定义,以及邻补角的定义是解题的关键.

练习册系列答案
相关题目
8.抛物线y=(x-1)(x+3)顶点坐标是( )
| A. | (2,5) | B. | (-22,-3) | C. | (1,0) | D. | (-1,-4) |
6.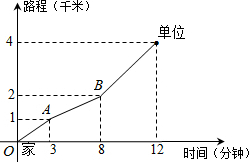 王老师从家门口骑车去单位上班,先走平路到达A地,再上坡到达B地,最后下坡到达工作单位,所用的时间与路程的关系如图所示.若王老师下班时,还沿着这条路返回家中,回家途中经过平路、上坡、下坡的速度不变,那么王老师回家需要的时间是( )
王老师从家门口骑车去单位上班,先走平路到达A地,再上坡到达B地,最后下坡到达工作单位,所用的时间与路程的关系如图所示.若王老师下班时,还沿着这条路返回家中,回家途中经过平路、上坡、下坡的速度不变,那么王老师回家需要的时间是( )
 王老师从家门口骑车去单位上班,先走平路到达A地,再上坡到达B地,最后下坡到达工作单位,所用的时间与路程的关系如图所示.若王老师下班时,还沿着这条路返回家中,回家途中经过平路、上坡、下坡的速度不变,那么王老师回家需要的时间是( )
王老师从家门口骑车去单位上班,先走平路到达A地,再上坡到达B地,最后下坡到达工作单位,所用的时间与路程的关系如图所示.若王老师下班时,还沿着这条路返回家中,回家途中经过平路、上坡、下坡的速度不变,那么王老师回家需要的时间是( )| A. | 15分钟 | B. | 14分钟 | C. | 13分钟 | D. | 12分钟 |
13.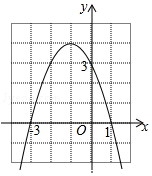 如图是二次函数y=ax2+bx+c的图象,下列结论错误的是( )
如图是二次函数y=ax2+bx+c的图象,下列结论错误的是( )
 如图是二次函数y=ax2+bx+c的图象,下列结论错误的是( )
如图是二次函数y=ax2+bx+c的图象,下列结论错误的是( )| A. | 二次函数y=ax2+bx+c的最大值为4 | |
| B. | 常数项c为3 | |
| C. | 一元二次方程ax2+bx+c=0的两根之和为-2 | |
| D. | 使y≤3成立的x的取值范围是x≥0 |
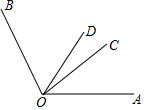 如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=25°,求∠AOB的度数.
如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=25°,求∠AOB的度数.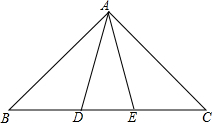 如图,△ABC中,AB=AC,点D,E在边BC上,且BD=CE.
如图,△ABC中,AB=AC,点D,E在边BC上,且BD=CE.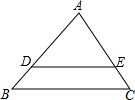 如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC,$\frac{AD}{BD}$=$\frac{3}{2}$,DE=6,则BC的长为( )
如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC,$\frac{AD}{BD}$=$\frac{3}{2}$,DE=6,则BC的长为( )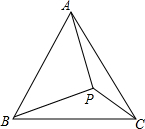 如图,P为等边三角形ABC内一点,PC=3,PA=4,PB=5,求∠APC的度数.
如图,P为等边三角形ABC内一点,PC=3,PA=4,PB=5,求∠APC的度数. 如图,在一块边长为a的正方形花圃中,两纵两横的4条宽度为b的人行道把花圃分成9块,下面是四个计算种花土地总面积的代数式:①(a-2b)(a-2b),②a2-4ab,③a2-4ab-4b2,④a2-4ab+4b2,其中正确的有( )
如图,在一块边长为a的正方形花圃中,两纵两横的4条宽度为b的人行道把花圃分成9块,下面是四个计算种花土地总面积的代数式:①(a-2b)(a-2b),②a2-4ab,③a2-4ab-4b2,④a2-4ab+4b2,其中正确的有( )