题目内容
9.已知抛物线y1=ax2+bx+c对称轴是直线l,顶点为M,若自变量x的函数值y1的部分对应值如表所示| x | … | -1 | 1 | 3 | … |
| y1=ax2+bx+c | … | 0 | 3 | 0 | … |
(2)若经过点T(0,t)作垂直于y轴的直线l′,A为直线l′上的动点,线段AM的垂直平分线交直线l于点B,点B关于直线AM的对称点为P,记作P(x,y2)
①用含x和t的代数式表示y2;
②当x取任意实数时,若对于同一个x,有y1<y2恒成立,求t的取值范围.
分析 (1)由题意抛物线与x轴交于点(-1,0),(3,0),设抛物线的解析式为y=a(x+1)(x-3),把(1,3)代入求出a即可.
(2)先根据(I)中y1与x之间的函数关系式得出顶点M的坐标.
①记直线l与直线l′交于点C(1,t),当点A′与点C不重合时,由已知得,AM与BP互相垂直平分,故可得出四边形ANMP为菱形,所以PA∥l,再由点P(x,y2)可知点A(x,t)(x≠1),所以PM=PA=|y2-t|,过点P作PQ⊥l于点Q,则点Q(1,y2),故QM=|y2-3|,PQ=AC=|x-1|,在Rt△PQM中,根据勾股定理即可得出y2与x之间的函数关系式,再由当点A与点C重合时,点B与点P重合可得出P点坐标,故可得出y2与x之间的函数关系式;
②根据题意,借助函数图象:当抛物线y2开口方向向上时,可知6-2t>0,即t<3时,抛物线y1的顶点M(1,3),抛物线y2的顶点(1,$\frac{t+3}{2}$),由于3>$\frac{t+3}{2}$,所以不合题意,当抛物线y2开口方向向下时,6-2t<0,即t>3时,求出y1-y2的值;若3t-11≠0,要使y1<y2恒成立,只要抛物线方向及顶点(1,$\frac{3-t}{2}$)在x轴下方,因为3-t<0,只要3t-11>0,解得t>$\frac{11}{3}$,符合题意;若3t-11=0,y1-y2=-$\frac{1}{3}$<0,即t=$\frac{11}{3}$也符合题意.
解答 解:(1)由题意抛物线与x轴交于点(-1,0),(3,0),设抛物线的解析式为y=a(x+1)(x-3),
把(1,3)代入得到a=-$\frac{3}{4}$,
∴抛物线的解析式为y=-$\frac{3}{4}$(x+1)(x-3),
即y=-$\frac{3}{4}$x2+$\frac{3}{2}$x+$\frac{9}{4}$.
(2))∵y1=-$\frac{3}{4}$x2+$\frac{3}{2}$x+$\frac{9}{4}$,
∴y1=-$\frac{3}{4}$(x-1)2+3,
∴直线l为x=1,顶点M(1,3).
①由题意得,t≠3,
如图,记直线l与直线l′交于点C(1,t),当点A与点C不重合时,
∵由已知得,AM与BP互相垂直平分,
∴四边形ABMP为菱形,
∴PA∥l,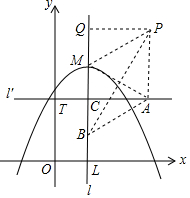
又∵点P(x,y2),
∴点A(x,t)(x≠1),
∴PM=PA=|y2-t|,
过点P作PQ⊥l于点Q,则点Q(1,y2),
∴QM=|y2-3|,PQ=AC=|x-1|,
在Rt△PQM中,
∵PM2=QM2+PQ2,即(y2-t)2=(y2-3)2+(x-1)2,整理得,y2=$\frac{1}{6-2t}$(x-1)2+$\frac{t+3}{2}$,
即y2=$\frac{1}{6-2t}$x2-$\frac{1}{3-t}$x+$\frac{10-{t}^{2}}{6-2t}$,
∵当点A与点C重合时,点B与点P重合,
∴P(1,$\frac{t+3}{2}$),
∴P点坐标也满足上式,
∴y2与x之间的函数关系式为y2=$\frac{1}{6-2t}$x2-$\frac{1}{3-t}$x+$\frac{10-{t}^{2}}{6-2t}$(t≠3);
②根据题意,借助函数图象:
当抛物线y2开口方向向上时,6-2t>0,即t<3时,抛物线y1的顶点M(1,3),抛物线y2的顶点(1,$\frac{t+3}{2}$),
∵3>$\frac{t+3}{2}$,
∴不合题意,
当抛物线y2开口方向向下时,6-2t<0,即t>3时,
y1-y2=-$\frac{3}{4}$(x-1)2+3-[$\frac{1}{6-2t}$(x-1)2+$\frac{t+3}{2}$]
=$\frac{3t-11}{4(3-t)}$(x-1)2+$\frac{3-t}{2}$,
若3t-11≠0,要使y1<y2恒成立,
只要抛物线y=$\frac{3t-11}{4(3-t)}$(x-1)2+$\frac{3-t}{2}$开口方向向下,且顶点(1,$\frac{3-t}{2}$)在x轴下方,
∵3-t<0,只要3t-11>0,解得t>$\frac{11}{3}$,符合题意;
若3t-11=0,y1-y2=-$\frac{1}{3}$<0,即t=$\frac{11}{3}$也符合题意.
综上,可以使y1<y2恒成立的t的取值范围是t≥$\frac{11}{3}$.
点评 本题考查的是二次函数综合题,涉及到待定系数法二次函数解的解析式、勾股定理及二次函数的性质,解答此类题目时要注意数形结合思想的运用.

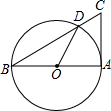 如图,AB是⊙O的直径,AC切⊙O于点A,BC交着⊙O于点D,连接OD,∠C=70°,则∠AOD的度数为40°.
如图,AB是⊙O的直径,AC切⊙O于点A,BC交着⊙O于点D,连接OD,∠C=70°,则∠AOD的度数为40°.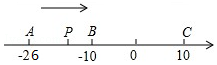 已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,以每秒1个单位的速度向右移动,当P点运动到C点时运动停止,设点P移动时间为t秒.
已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,以每秒1个单位的速度向右移动,当P点运动到C点时运动停止,设点P移动时间为t秒.