题目内容
4．
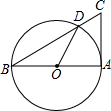如图，AB是⊙O的直径，AC切⊙O于点A，BC交着⊙O于点D，连接OD，∠C=70°，则∠AOD的度数为40°．
分析 由AB是⊙O的直径，AC切⊙O于点A，可得AB⊥AC，又由∠C=70°，可求得∠B的度数，然后由圆周角定理，求得答案．
解答 解：∵AB是⊙O的直径，AC切⊙O于点A，
∴AB⊥AC，
∵∠C=70°，
∴∠B=90°-∠C=20°，
∴∠AOD=2∠B=40°．
故答案为：40°．
点评 此题考查了切线的性质以及圆周角定理．注意圆的切线垂直于经过切点的半径．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．先化简，再求值：
①6x-5y+3y-2x，其中x=-2，y=-3．
②$\frac{1}{4}$（-4a2+2a-8）-（$\frac{1}{2}$a-2），其中a=-$\frac{1}{2}$．
①6x-5y+3y-2x，其中x=-2，y=-3．
②$\frac{1}{4}$（-4a2+2a-8）-（$\frac{1}{2}$a-2），其中a=-$\frac{1}{2}$．
15．下列各图中，一定全等的是（ ）
| A． | 顶角相等的两个等腰三角形 | |
| B． | 有两边和一角分别相等的等腰三角形 | |
| C． | 各有一个角是45°，腰长都是3cm的两个等腰三角形 | |
| D． | 底边和顶角都相等的两个等腰三角形 |
12．两个非零有理数a，b互为相反数，则下列说法错误的是（ ）
| A． | a+b=0 | B． | a3=b3 | C． | a2=b2 | D． | $\frac{a}{b}=-1$ |
9．已知抛物线y1=ax2+bx+c对称轴是直线l，顶点为M，若自变量x的函数值y1的部分对应值如表所示
（1）求y1与x之间的函数关系式；
（2）若经过点T（0，t）作垂直于y轴的直线l′，A为直线l′上的动点，线段AM的垂直平分线交直线l于点B，点B关于直线AM的对称点为P，记作P（x，y2）
①用含x和t的代数式表示y2；
②当x取任意实数时，若对于同一个x，有y1＜y2恒成立，求t的取值范围．
| x | … | -1 | 1 | 3 | … |
| y1=ax2+bx+c | … | 0 | 3 | 0 | … |
（2）若经过点T（0，t）作垂直于y轴的直线l′，A为直线l′上的动点，线段AM的垂直平分线交直线l于点B，点B关于直线AM的对称点为P，记作P（x，y2）
①用含x和t的代数式表示y2；
②当x取任意实数时，若对于同一个x，有y1＜y2恒成立，求t的取值范围．
13．下列各组数中，相等的一组是（ ）
| A． | （-2）3和-（-23） | B． | -（-2）和-|-2| | C． | （-2）2和-（-22） | D． | |-2|3和-|2|3 |