题目内容
对下列问题,有三位同学提出了各自的想法:
若方程组
的解是
,求方程组
的解.甲说:“这个题目的好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以4,通过换元替代的方法来解决”.参考他们的讨论,请你探索:若能求解,请求出它的解;若不能,请说明理由.答: .
若方程组
|
|
|
考点:二元一次方程组的解
专题:
分析:把第二个方程组的两个方程的两边都除以4,通过换元替代的方法即可得到一个关于x,y的方程组,即可求解.
解答:解:第二个方程组的两个方程的两边都除以4得:
,
∴
,
解得:
,
故答案为:
.
|
∴
|
解得:
|
故答案为:
|
点评:本题主要考查了方程组的解法,正确观察已知方程的系数之间的关系是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 如图,这是某市部分简图,为了确定各建筑物的位置:
如图,这是某市部分简图,为了确定各建筑物的位置: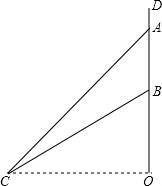 如图,水渠边有一颗大木瓜树,树干DO(不计粗细)上有两个木瓜A、B(不计大小),树干垂直于地面,量得AB=2米,在水渠的对面与O处于同一水平面的C处测得木瓜A的仰角为45°、木瓜B的仰角为30°,求C处到树干DO的距离CO.(保留根号即可)
如图,水渠边有一颗大木瓜树,树干DO(不计粗细)上有两个木瓜A、B(不计大小),树干垂直于地面,量得AB=2米,在水渠的对面与O处于同一水平面的C处测得木瓜A的仰角为45°、木瓜B的仰角为30°,求C处到树干DO的距离CO.(保留根号即可) 如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个动点到达终点时,另一个动点也随之停止运动.
如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个动点到达终点时,另一个动点也随之停止运动. 光华中学部分学生举行投篮比赛,每人投篮10次.如图是将比赛结果整理后,画出的频数分布直方图,则投篮命中数在5次及以上的学生与参赛人数的比是
光华中学部分学生举行投篮比赛,每人投篮10次.如图是将比赛结果整理后,画出的频数分布直方图,则投篮命中数在5次及以上的学生与参赛人数的比是