题目内容
1．已知一盒子中装有6个完全相同的小球，上面分别标有1，2，3，4，5，6，搅匀后从中摸出一个小球（不放回），其上数字记作点P的横坐标，然后再摸出一个小球，其上数字记作点P的纵坐标，则点P落在直线y=2x-4和y=-x+8与x轴围成的封闭区域内（含边界）的概率是$\frac{1}{3}$．分析 首先根据题意列出表格，然后由表格即可求得所有等可能的结果与点P落在直线y=2x-4和y=-x+8与x轴围成的封闭区域内（含边界）的情况，再利用概率公式即可求得答案．
解答 解：列表得：
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | （2，1） | （3，1） | （4，1） | （5，1） | （6，1） | |
| 2 | （1，2） | （3，2） | （4，2） | （5，2）（ | （6，2） | |
| 3 | （1，3） | （2，3） | （4，3） | （5，3） | （6，3） | |
| 4 | （1，4） | （2，4） | （3，4） | （5，4） | （6，4） | |
| 5 | （1，5） | （2，5） | （3，5） | （4，5） | （6，5） | |
| 6 | （1，6） | （2，6） | （3，6） | （4，6） | （5，6） |
∴点P落在直线y=2x-4和y=-x+8与x轴围成的封闭区域内（含边界）的概率是：$\frac{10}{30}$=$\frac{1}{3}$．
故答案为：$\frac{1}{3}$．
点评 此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
如图，在△ABC中，∠A=60°，∠B=45°，AC=8，CD⊥AB，垂足为点D，求AB的长．
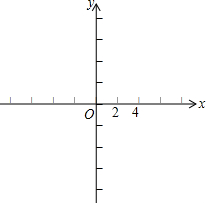如图，在下面的平面直角坐标系中，作出以A（1，2），B（3，1），C（4，4）为顶点的三角形，并在第一象限内作出它的位似三角形A′B′C′，使原三角形与新三角形的位似比为2：1，位似中心是圆点．
如图，在?ABCD中，E是AD边的中点，EC交对角线BD于F，则EF：FC=1：2；△DFC的面积为8，则△DEF的面积为4．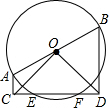
如图，已知AB是⊙O的直径，EF为弦，AC、BD垂直于EF所在直线，C、D为垂足．求证：OC=OD，CE=DF．
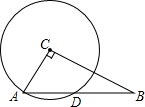如图所示，已知在Rt△ABC，∠ACB=90°，AC=5cm，BC=12cm，以点C为圆心，CA为半径的圆交斜边于点D，求AD的长．
如图，将长方形ABCD沿AC折叠，使点B落在点E处，则图中全等三角形共有3对（包括虚线）