题目内容
10.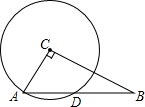 如图所示,已知在Rt△ABC,∠ACB=90°,AC=5cm,BC=12cm,以点C为圆心,CA为半径的圆交斜边于点D,求AD的长.
如图所示,已知在Rt△ABC,∠ACB=90°,AC=5cm,BC=12cm,以点C为圆心,CA为半径的圆交斜边于点D,求AD的长.
分析 过C作CE⊥AB于E,根据垂径定理得出AD=2AE,根据勾股定理求AB,根据射影定理求出AE,即可求出AD的长.
解答  解:过C作CE⊥AB于E,
解:过C作CE⊥AB于E,
∵CE⊥AB,CE过圆心C,
∴AD=2AE.
∵△ABC中,∠C是直角,AC=5cm,BC=12cm,
∴由勾股定理得:AB=13cm,
由射影定理得:AC2=AE×AB,
∴AE=$\frac{25}{13}$,
∴AD=2AE=$\frac{50}{13}$cm.
点评 本题考查了垂径定理,射影定理,勾股定理等知识点的应用,关键是求出AE的长,主要培养学生运用定理进行推理的能力,题目比较典型,难度适中.

练习册系列答案
相关题目
5.如果把分式$\frac{xy}{4x-3y}$中的x和y的值都扩大2倍,那么分式的值( )
| A. | 扩大2倍 | B. | 缩小2倍 | C. | 不改变 | D. | 扩大4倍 |
4.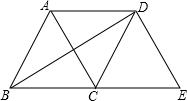 如图所示,等边三角形ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:(1)AD=BC(2)BD与AC互相平分(3)四边形ACED是菱形,其中正确的个数是( )
如图所示,等边三角形ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:(1)AD=BC(2)BD与AC互相平分(3)四边形ACED是菱形,其中正确的个数是( )
 如图所示,等边三角形ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:(1)AD=BC(2)BD与AC互相平分(3)四边形ACED是菱形,其中正确的个数是( )
如图所示,等边三角形ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:(1)AD=BC(2)BD与AC互相平分(3)四边形ACED是菱形,其中正确的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
1.下列结论正确的是( )
| A. | -1乘以一个数得到这个数的相反数 | B. | |-$\frac{1}{7}$|×$\frac{1}{7}$=-$\frac{1}{49}$ | ||
| C. | -$\frac{1}{3}$×3=1 | D. | 几个有理数相乘,同号得正 |
2.若方程(x+2)(3x-a)=3x2-bx+4,则( )
| A. | a=2,b=4 | B. | a=-2,b=4 | C. | a=2,b=-8 | D. | a=-2,b=-8 |
 如图,直线AB、CD、EF相交于点O,若∠1与∠2互为余角,则CD⊥EF.请说明理由.
如图,直线AB、CD、EF相交于点O,若∠1与∠2互为余角,则CD⊥EF.请说明理由.