题目内容
16.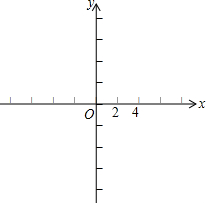 如图,在下面的平面直角坐标系中,作出以A(1,2),B(3,1),C(4,4)为顶点的三角形,并在第一象限内作出它的位似三角形A′B′C′,使原三角形与新三角形的位似比为2:1,位似中心是圆点.
如图,在下面的平面直角坐标系中,作出以A(1,2),B(3,1),C(4,4)为顶点的三角形,并在第一象限内作出它的位似三角形A′B′C′,使原三角形与新三角形的位似比为2:1,位似中心是圆点.
分析 根据位似变换中对应点的坐标特征,把点A、B、C的横纵坐标都乘以$\frac{1}{2}$得到点A′($\frac{1}{2}$,1),B′($\frac{3}{2}$,$\frac{1}{2}$),C′(2,2),然后描点即可得到△ABC和△A′B′C′.
解答 解:如图,△ABC和△A′B′C′为所作.
点评 本题考查了作图-位似变换:画位似图形的一般步骤为:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;然后根据位似比,确定能代表所作的位似图形的关键点;最后顺次连接上述各点,得到放大或缩小的图形.

练习册系列答案
相关题目
5.如果把分式$\frac{xy}{4x-3y}$中的x和y的值都扩大2倍,那么分式的值( )
| A. | 扩大2倍 | B. | 缩小2倍 | C. | 不改变 | D. | 扩大4倍 |
 小王骑车从甲地到乙地,小季骑车从乙地到甲地,两人同时出发,沿同一条公路匀速前进,小王的速度小于小李的速度,在出发2h时,两人相距36km,在出发4h时,两人又相距36km,设小王骑行的时间为x(h),两人之间的距离为y(km),图中的折线表示y与x之间的函数关系.
小王骑车从甲地到乙地,小季骑车从乙地到甲地,两人同时出发,沿同一条公路匀速前进,小王的速度小于小李的速度,在出发2h时,两人相距36km,在出发4h时,两人又相距36km,设小王骑行的时间为x(h),两人之间的距离为y(km),图中的折线表示y与x之间的函数关系.