题目内容
17．已知菱形的周长是20cm，一条对角线长是6cm，则这个菱形面积为（ ）| A． | 48cm2 | B． | 30cm2 | C． | 24cm2 | D． | 25cm2 |
分析 根据菱形的性质，先求另一条对角线的长度，再运用菱形的面积等于对角线乘积的一半求解．
解答 
解：如图，在菱形ABCD中，BD=6cm．
∵菱形的周长为20cm，BD=6cm，
∴AB=5cm，BO=3cm，
∴AO=$\sqrt{{5}^{2}-{3}^{2}}$=4（cm），AC=8cm．
∴面积S=$\frac{1}{2}$×6×8=24（cm2）．
故选：C．
点评 本题考查了菱形的对角线互相垂直平分的性质，菱形的面积等于对角线乘积的一半，勾股定理的应用，熟记性质是解题的关键．
练习册系列答案
相关题目
8．
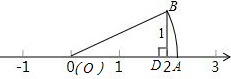如图，OA=OB，BD=1，则数轴上点A所表示的数为（ ）
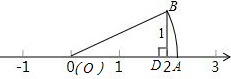如图，OA=OB，BD=1，则数轴上点A所表示的数为（ ）| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\sqrt{5}$ | D． | $\sqrt{10}$ |
2．已知直角三角形两条直角边的和是$\sqrt{6}$，斜边上的中线长为1，则这个三角形的面积等于（ ）
| A． | 2$\sqrt{3}$ | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
如图，已知?ABCD的周长为80cm，对角线AC与BD相交于点O，△AOB的周长比△AOD的周长小20cm，求AB和AD的长．
如图，在?ABCD中，AM⊥BC于M，AN⊥CD于N．求证：AC•AM=MN•AB．