题目内容
8．
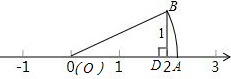如图，OA=OB，BD=1，则数轴上点A所表示的数为（ ）| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\sqrt{5}$ | D． | $\sqrt{10}$ |
分析 根据勾股定理，可得OB的长，根据圆的半径相等，可得OA的长．
解答 解：由勾股定理，得
OB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
由圆的半径相等，得
OA=$\sqrt{5}$，
故选：C．
点评 本题考查了实数与数轴，利用勾股定理得出OB的长是解题关键．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
16．
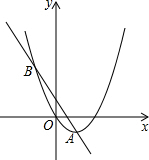如图，已知抛物线y1=$\frac{1}{2}$x2-2x，直线y2=-2x+b相交于A、B两点，其中点A的横坐标为2，当x任取一值时，x对应的函数值分别为y1、y2，取m=$\frac{1}{2}$（|y1-y2|+y1+y2）则（ ）
如图，已知抛物线y1=$\frac{1}{2}$x2-2x，直线y2=-2x+b相交于A、B两点，其中点A的横坐标为2，当x任取一值时，x对应的函数值分别为y1、y2，取m=$\frac{1}{2}$（|y1-y2|+y1+y2）则（ ）| A． | 点B的坐标随b的值的变化而变化 | B． | m随x的增大而减小 | ||
| C． | 当m=2时，x=0 | D． | m≥-2 |
如图所示，在△ABC中，∠C=90°，D为边AB上一点，且BD=BC，ED⊥AB，垂足为D，如果AC=10，那么AE+DE=10．
20．下列各组量中，不是具有相反意义的量是（ ）
| A． | 向南走100米和向北走50米 | B． | 零上10℃和零下2℃ | ||
| C． | 赢了10局和输了5局 | D． | 伸长10厘米和减少3千克 |
17．已知菱形的周长是20cm，一条对角线长是6cm，则这个菱形面积为（ ）
| A． | 48cm2 | B． | 30cm2 | C． | 24cm2 | D． | 25cm2 |