题目内容
1.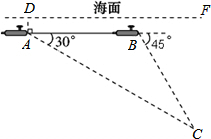 如图,一艘核潜艇在海面DF下615米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1 025米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,一艘核潜艇在海面DF下615米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1 025米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
分析 首先作CE⊥AB于E,依题意,AB=1025,∠EAC=30°,∠CBE=45°,设CE=x,则BE=x,进而利用正切函数的定义求出x即可.
解答 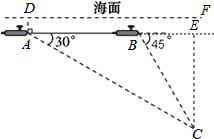 解:作CE⊥AB于E,
解:作CE⊥AB于E,
依题意,AB=1025,∠EAC=30°,∠CBE=45°,
设CE=x,则BE=x,
Rt△ACE中,tan30°=$\frac{CE}{AE}$=$\frac{x}{1025+x}$=$\frac{\sqrt{3}}{3}$,
整理得出:3x=1025$\sqrt{3}$+$\sqrt{3}$x,
解得:x=$\frac{1025}{2}$($\sqrt{3}$+1)≈1400.15米,
则海底C点处距离海面DF的深度=x+615≈2015米.
答:海底C点处距离海面DF的深度约为2015米.
点评 此题主要考查了俯角的定义及其解直角三角形的应用,解题时首先正确理解俯角的定义,然后利用三角函数和已知条件构造方程解决问题.

练习册系列答案
相关题目
11.方程x2=2x的解是( )
| A. | x=2 | B. | x1=2,x2=0 | C. | x1=$\sqrt{2}$,x2=0 | D. | x=0 |
9.地球上的海洋面积约为36100000km2,用科学记数法可表示为( )
| A. | 3.61×106km2 | B. | 3.61×107km2 | C. | 0.361×108km2 | D. | 3.61×109km2 |
16.学校团委在“五四”青年节举行“校园之星”颁奖活动中,九(1)班决定从甲、乙、丙、丁四人中随机派两名代表参加此活动,则所选两名代表恰好是甲和乙的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
13.据统计,今年五一小长假某景区共接待游客35000多名,35000写成科学记数法为( )
| A. | 35×103 | B. | 3.5×104 | C. | 0.35×105 | D. | 3.5×103 |
 如图所示,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠BAD=120°,BE=2,FD=3,则∠EAF=60°,?ABCD的周长为20.
如图所示,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠BAD=120°,BE=2,FD=3,则∠EAF=60°,?ABCD的周长为20.