题目内容
7.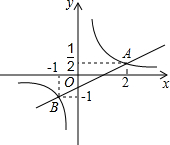 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于A(2,$\frac{1}{2}$),B(-1,1)两点.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于A(2,$\frac{1}{2}$),B(-1,1)两点.(1)分别求出反比例函数和一次函数的解析式;
(2)根据图象写出:当x为何值时,一次函数值大于反比例函数值.
分析 (1)根据图象可直接得出x的取值范围;
(2)将点A、B代入一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)可得出m,k、b,从而得出两个解析式.
解答 解:(1)把A(2,$\frac{1}{2}$)代入y=$\frac{m}{x}$,得m=1,
∴反比例函数的解析式为y=$\frac{1}{x}$,
把A(2,$\frac{1}{2}$),B(-1,-1)两点代入y=kx+b,
得$\left\{\begin{array}{l}{2k+b=\frac{1}{2}}\\{-k+b=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$.
故一次函数的解析式为y=$\frac{1}{2}$x-$\frac{1}{2}$;
(2)由图象可知:当x>2或-1<x<0时,一次函数值大于反比例函数值.
点评 本题考查了反比例函数和一次函数的交点问题,用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.这里体现了数形结合的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.学校团委在“五四”青年节举行“校园之星”颁奖活动中,九(1)班决定从甲、乙、丙、丁四人中随机派两名代表参加此活动,则所选两名代表恰好是甲和乙的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
 (1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$;
(1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$; △ABC中,∠B=30°,AB=8cm,BC=4cm,则△ABC的面积为8cm2.
△ABC中,∠B=30°,AB=8cm,BC=4cm,则△ABC的面积为8cm2. 如图所示,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠BAD=120°,BE=2,FD=3,则∠EAF=60°,?ABCD的周长为20.
如图所示,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠BAD=120°,BE=2,FD=3,则∠EAF=60°,?ABCD的周长为20.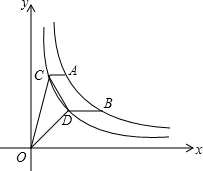 如图,点A、B在双曲线y1=$\frac{k}{x}$(k>1,x>0)上,点C、点D在双曲线y2=$\frac{1}{x}$(x>0)上,AC∥BD∥x轴,若$\frac{AC}{BD}$=m,则△OCD的面积为$\frac{1-{m}^{2}}{2m}$.(用含m的式子表示)
如图,点A、B在双曲线y1=$\frac{k}{x}$(k>1,x>0)上,点C、点D在双曲线y2=$\frac{1}{x}$(x>0)上,AC∥BD∥x轴,若$\frac{AC}{BD}$=m,则△OCD的面积为$\frac{1-{m}^{2}}{2m}$.(用含m的式子表示)