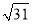题目内容
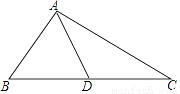
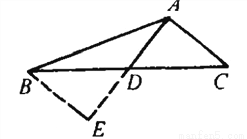
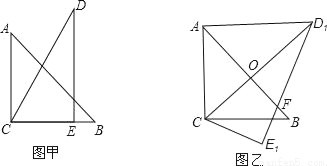
如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=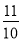 ,则tan∠BAD=________.
,则tan∠BAD=________.
【答案】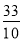
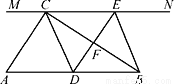
【解析】延长AD到E,使AD=DE,CF 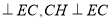 ,
,
在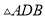 与
与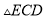 ,
,
,  ,所以
,所以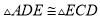 ,
,
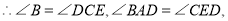
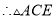 是等腰三角形,s
是等腰三角形,s
设EM= x,DE=11,MC=10,
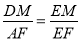 ,
,
 ,
,
 x=
x=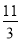 ,
,
 tan∠BAD=
tan∠BAD=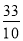 .
.
故答案为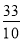 .
.
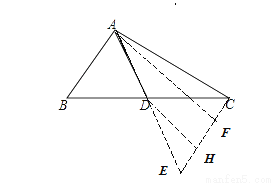
点睛:倍长中线法构造全等三角形,如图,AD是中线,令AD=DE,则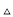 ADC全等
ADC全等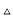 EBD.
EBD.
【题型】填空题
【结束】
21
先化简,再求值: 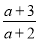 ÷(
÷(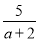 -a+2),其中a=2sin60°+3tan45°.
-a+2),其中a=2sin60°+3tan45°.
练习册系列答案
相关题目



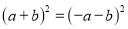 B.
B. 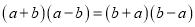
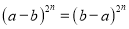 D.
D. 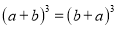
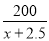 =2×
=2×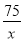 ,
,
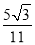 ,EG=2,求AE的长.
,EG=2,求AE的长.

 B. 5 C. 4 D.
B. 5 C. 4 D.