题目内容
某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
【答案】(1)A种品牌套装每套进价为10元,B种品牌套装每套进价为7.5元;(2)最少购进A品牌工具套装17套.
【解析】试题分析:(1)利用两种套装的套数作为等量关系列方程求解.(2)利用总获利大于等于120,解不等式.
试题解析:
(1)【解析】
设B种品牌套装每套进价为x元,则A种品牌套装每套进价为(x+2.5)元.
根据题意得: 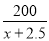 =2×
=2×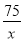 ,
,
解得:x=7.5,
经检验,x=7.5为分式方程的解,
∴x+2.5=10.
答:A种品牌套装每套进价为10元,B种品牌套装每套进价为7.5元.
(2)【解析】
设购进A品牌工具套装a套,则购进B品牌工具套装(2a+4)套,
根据题意得:(13﹣10)a+(9.5﹣7.5)(2a+4)>120,
解得:a>16,
∵a为正整数,
∴a取最小值17.
答:最少购进A品牌工具套装17套.
点睛:分式方程应用题:一设,一般题里有两个有关联的未知量,先设出一个未知量,并找出两个未知量的联系;二列,找等量关系,列方程,这个时候应该注意的是和差分倍关系:三解,正确解分式方程;四验,应用题要双检验;五答,应用题要写答.
【题型】解答题
【结束】
26
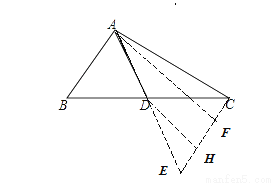
四边形ABCD内接于⊙O,点E为AD上一点,连接AC,CB,∠B=∠AEC.
(1)如图1,求证:CE=CD;
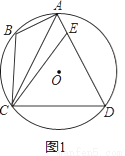
(2)如图2,若∠B+∠CAE=120°,∠ACD=2∠BAC,求∠BAD的度数;
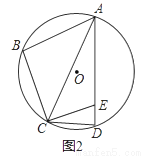
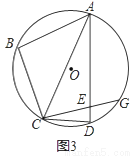
(3)如图3,在(2)的条件下,延长CE交⊙O于点G,若tan∠BAC= 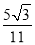 ,EG=2,求AE的长.
,EG=2,求AE的长.


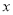 ,则下列方程不正确的是( )
,则下列方程不正确的是( )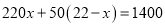 B.
B. 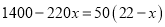
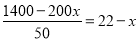 D.
D. 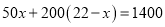
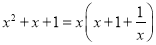
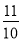 ,则tan∠BAD=________.
,则tan∠BAD=________.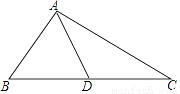
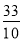
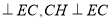 ,
,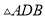 与
与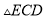 ,
, ,所以
,所以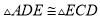 ,
,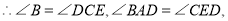
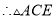 是等腰三角形,s
是等腰三角形,s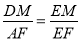 ,
, ,
, x=
x=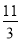 ,
, tan∠BAD=
tan∠BAD=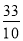 .
.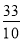 .
.
 ADC全等
ADC全等 EBD.
EBD.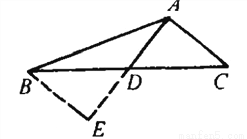
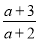 ÷(
÷(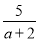 -a+2),其中a=2sin60°+3tan45°.
-a+2),其中a=2sin60°+3tan45°.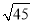 ﹣
﹣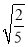 ×
×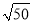 =________.
=________.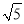
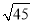 ﹣
﹣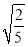 ×
×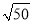 =3
=3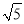 -2
-2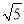 =
=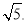
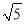 .
.