题目内容
20.在平面直角坐标系xOy中,A(1,2),B(3,2),连接AB.写出一个函数y=$\frac{k}{x}$(k≠0),使它的图象与线段AB有公共点,那么这个函数的表达式为y=$\frac{2}{x}$.分析 把线段AB上的任意一点的坐标代入y=$\frac{k}{x}$可求出k,从而得到满足条件的反比例函数解析式.
解答 解:把A(1,2)代入y=$\frac{k}{x}$得k=1×2,
所以经过点A的反比例函数解析式为y=$\frac{2}{x}$.
故答案为y=$\frac{2}{x}$.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
8.下列分式变形正确的是( )
| A. | $\frac{4}{{x}^{2}}$=$\frac{2}{x}$ | B. | $\frac{-x+1}{x+1}$=-1 | ||
| C. | $\frac{2x}{4x-6}$=$\frac{x}{2x-3}$ | D. | 1-$\frac{x+1}{x-2}$=$\frac{x-2-x+1}{x-2}$ |
5. 如图,分别过点P(i,0)(i=1、2、…n)作x轴的垂线,交y=$\frac{1}{2}$x2的图象于点A,交直线y=-$\frac{1}{2}$x于点Bi,则$\frac{1}{{A}_{1}{B}_{1}}$+$\frac{1}{{A}_{2}{B}_{2}}$+…+$\frac{1}{{A}_{n}{B}_{n}}$等于( )
如图,分别过点P(i,0)(i=1、2、…n)作x轴的垂线,交y=$\frac{1}{2}$x2的图象于点A,交直线y=-$\frac{1}{2}$x于点Bi,则$\frac{1}{{A}_{1}{B}_{1}}$+$\frac{1}{{A}_{2}{B}_{2}}$+…+$\frac{1}{{A}_{n}{B}_{n}}$等于( )
 如图,分别过点P(i,0)(i=1、2、…n)作x轴的垂线,交y=$\frac{1}{2}$x2的图象于点A,交直线y=-$\frac{1}{2}$x于点Bi,则$\frac{1}{{A}_{1}{B}_{1}}$+$\frac{1}{{A}_{2}{B}_{2}}$+…+$\frac{1}{{A}_{n}{B}_{n}}$等于( )
如图,分别过点P(i,0)(i=1、2、…n)作x轴的垂线,交y=$\frac{1}{2}$x2的图象于点A,交直线y=-$\frac{1}{2}$x于点Bi,则$\frac{1}{{A}_{1}{B}_{1}}$+$\frac{1}{{A}_{2}{B}_{2}}$+…+$\frac{1}{{A}_{n}{B}_{n}}$等于( )| A. | $\frac{2n}{n}$ | B. | $\frac{2n}{n+1}$ | C. | $\frac{2n}{n-1}$ | D. | $\frac{n}{n-1}$ |
12. 如图,在△ABC中,AB=AC,高BD,CE交于点O,AO交BC于点F,则图中共有全等三角形( )
如图,在△ABC中,AB=AC,高BD,CE交于点O,AO交BC于点F,则图中共有全等三角形( )
 如图,在△ABC中,AB=AC,高BD,CE交于点O,AO交BC于点F,则图中共有全等三角形( )
如图,在△ABC中,AB=AC,高BD,CE交于点O,AO交BC于点F,则图中共有全等三角形( )| A. | 8对 | B. | 7对 | C. | 6对 | D. | 5对 |
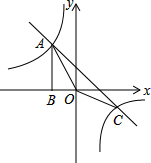 如图,点A、点C是双曲线y1=$\frac{{k}_{1}}{x}$与直线y2=-x+k2-1的两个交点,AB⊥x轴于点B,且S△ABO=2.
如图,点A、点C是双曲线y1=$\frac{{k}_{1}}{x}$与直线y2=-x+k2-1的两个交点,AB⊥x轴于点B,且S△ABO=2.