题目内容
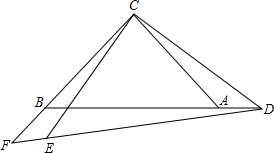等腰直角△ABC中，∠ACB=90°，AC=BC，点D是斜边AB上一点，以CD为直角边作等腰直角△CDE，其中∠DCE=90°，CD=CE，直线BC、DE交于点F．当点D在BA的延长线上时，若AB=kAD，求DF与EF的数量关系．（用含k的式子表示）考点：相似三角形的判定与性质
专题：
分析：首先证明△CAD∽△CEF，△BCA∽△ECA，根据相似三角新的对应边的比相等即可证得
=
，从而求解．
| AD |
| EF |
| AB |
| ED |
解答：解：∵△BCA和△ECD都是等腰直角三角形，
∴得∠FCE=∠ACD，∠CEF=∠CAD=135°，
∴△CAD∽△CEF，
∴
=
，
又∵△BCA∽△ECA，
∴
=
=
，
∴
=
，
∴
=
（分子比分子，等于分母比分母），
又∵AB=kAD，
∴DE=kEF，
∴DF=（k+1）EF．
∴得∠FCE=∠ACD，∠CEF=∠CAD=135°，
∴△CAD∽△CEF，
∴
| AD |
| EF |
| CA |
| CE |
又∵△BCA∽△ECA，
∴
| BA |
| ED |
| CA |
| CD |
| CA |
| CE |
∴
| AD |
| EF |
| AB |
| ED |
∴
| AD |
| AB |
| EF |
| DF |
又∵AB=kAD，
∴DE=kEF，
∴DF=（k+1）EF．
点评：本题考查相似三角形的判定与性质，相似三角形的对应边的比相等，根据等量代换得到
=
是关键．
| AD |
| EF |
| AB |
| ED |
练习册系列答案
相关题目
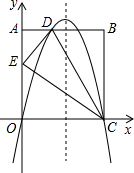如图，在矩形OABC中，点A（0，10），C（8，0）．沿直线CD折叠矩形OABC的一边BC，使点B落在OA边上的点E处．分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系，抛物线y=ax2+bx+c经过O，D，C三点．
“十•一”黄金周期间，某风景区在7天假期中每天旅游的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）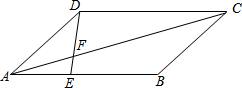
已知如图：?ABCD中，AE：EB=1：2，S△AEF=6cm2