题目内容
15.观察下面的一列二次根式,并填空:| 第1个 | 第2个 | 第3个 | 第4个 | … |
| $\sqrt{{1^2}+1}$ | $\sqrt{{2^2}+2}$ | $\sqrt{{3^2}+3}$ | $\sqrt{{4^2}+4}$ | … |
(2)通过观察估算:第16个二次根式的值在16和17这两个连续正数之间.
分析 (1)由表中几个式子和第几个之间的关系,不难表示出:第n个二次根式为$\sqrt{{n}^{2}+n}$;
(2)根据规律,第16个二次根式为$\sqrt{1{6}^{2}+16}$=$\sqrt{16×17}$.因为256<272<289,所以可求得16<$\sqrt{272}$<17.
解答 解:(1)根据题意可知第n个二次根式为$\sqrt{{n}^{2}+n}$.
故答案为$\sqrt{{n}^{2}+n}$;
(2)因为256<272<289,
所以可求得16<$\sqrt{272}$<17.
故答案为16.
点评 此题主要考查了无理数的估算,也是一个找规律的题目,首先根据表格找出规律,再根据规律计算特殊值,最后利用平方进行正确估算.本题的关键是得出第n个二次根式为$\sqrt{{n}^{2}+n}$.

练习册系列答案
相关题目
5. 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )| A. | cosC=$\frac{CD}{AC}$ | B. | cosC=$\frac{AC}{BC}$ | C. | cosC=$\frac{AD}{AC}$ | D. | cosC=$\frac{AD}{AB}$ |
3.若分式$\frac{{x}^{2}-9}{x-3}$的值为0,则x的值等于( )
| A. | 0 | B. | ±3 | C. | 3 | D. | -3 |
4.一名射击运动员,射靶10次,射击成绩分别为(单位:环):9,10,8,7,7,8,9,10,9,8,则他射中9环及9环以上的频率为( )
| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
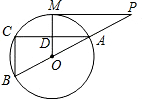 如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,交OM于点D.
如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,交OM于点D. 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2).
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2).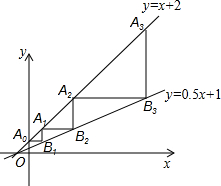 如图,直线y=x+2与y轴相交于点A0,过点A0作x轴的平行线交直线y=0.5x+1于点B1,过点B1作y轴的平行线交直线y=x+2于点A1,再过点A1作x轴的平行线交直线y=0.5x+1于点B2,过点B2作y轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x+1上的点B1,B2,B3,…,则An-1Bn的长为2n.
如图,直线y=x+2与y轴相交于点A0,过点A0作x轴的平行线交直线y=0.5x+1于点B1,过点B1作y轴的平行线交直线y=x+2于点A1,再过点A1作x轴的平行线交直线y=0.5x+1于点B2,过点B2作y轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x+1上的点B1,B2,B3,…,则An-1Bn的长为2n.