题目内容
因式分解:
(1)5ab+10a2b;
(2)x4-81;
(3)4x2-4xy+y2-a2.
(4)m4+16n4-8m2n2.
(1)5ab+10a2b;
(2)x4-81;
(3)4x2-4xy+y2-a2.
(4)m4+16n4-8m2n2.
考点:提公因式法与公式法的综合运用,因式分解-分组分解法
专题:
分析:(1)直接提取公因式5ab,进而得出答案;
(2)直接利用平方差公式分解因式即可,注意分解因式要彻底;
(3)首先将前三项组合,利用完全平方公式以及平方差公式分解因式得出即可;
(4)首先利用完全平方公式分解因式,进而利用平方差公式分解因式即可.
(2)直接利用平方差公式分解因式即可,注意分解因式要彻底;
(3)首先将前三项组合,利用完全平方公式以及平方差公式分解因式得出即可;
(4)首先利用完全平方公式分解因式,进而利用平方差公式分解因式即可.
解答:解:(1)5ab+10a2b=5ab(1+2a);
(2)x4-81=(x2+9)(x2-9)=(x2+9)(x+3)(x-3);
(3)4x2-4xy+y2-a2
=(2x-y)2-a2
=(2x-y+a)(2x-y-a);
(4)m4+16n4-8m2n2
=(m2-4n2)2
=(m+2n)2(m-2n)2.
(2)x4-81=(x2+9)(x2-9)=(x2+9)(x+3)(x-3);
(3)4x2-4xy+y2-a2
=(2x-y)2-a2
=(2x-y+a)(2x-y-a);
(4)m4+16n4-8m2n2
=(m2-4n2)2
=(m+2n)2(m-2n)2.
点评:此题主要考查了提取公因式法以及公式法分解因式,熟练利用平方差公式进行分解是解题关键.

练习册系列答案
相关题目
若不等式组
无解,则m的取值范围是( )
|
| A、m>4 | B、m<4 |
| C、m≥4 | D、m≤4 |

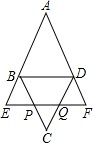 如图,在?ABCD中,点E、F分别在AB、AD延长线上,使得EF∥BD,连接EF,分别交BC、CD于点P、Q,已知BE=BP.求证:
如图,在?ABCD中,点E、F分别在AB、AD延长线上,使得EF∥BD,连接EF,分别交BC、CD于点P、Q,已知BE=BP.求证:
 如图,在边长为a的正方形ABCD中,点 G、M分别为AD、AB的中点,MN⊥MD,BN平分∠CBE并交MN于N.
如图,在边长为a的正方形ABCD中,点 G、M分别为AD、AB的中点,MN⊥MD,BN平分∠CBE并交MN于N. 如图,AB∥CD,∠α=50°,∠D=∠C,依次求出∠D,∠C,∠B的度数.
如图,AB∥CD,∠α=50°,∠D=∠C,依次求出∠D,∠C,∠B的度数.