题目内容
19.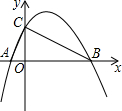 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点,与y轴交与点C,⊙O′为△ABC的外接圆.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点,与y轴交与点C,⊙O′为△ABC的外接圆.(1)求圆心O′的坐标;
(2)求⊙O′与抛物线的第四个交点D的坐标.
分析 (1)根据抛物线与x轴的交点问题,通过解方程-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=0得到A(-1,0),B(4,0),则计算自变量为0时的函数值得到C点坐标,再利用勾股定理的逆定理可证明△ACB为直角三角形,∠ACB=90°,则根据圆周角定理的推论可判断AB为△ABC的外接圆的直径,写出AB的中点坐标即可得到圆心O′的坐标;
(2)利用圆和抛物线的对称性可判断⊙O′与抛物线的第四个交点D与点C关于直线x=1.5对称,于是可得到点D的坐标.
解答 解:(1)当y=0时,-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=0,解得x1=-1,x2=4,则A(-1,0),B(4,0),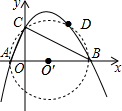
当x=0时,y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=2,则C(0,2),
∵AB=4-(-1)=5,AC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴AC2+BC2=AB2,
∴△ACB为直角三角形,∠ACB=90°,
∴AB为△ABC的外接圆的直径,即AB为⊙O′的直径,
∴圆心O′的坐标(1.5,0);
(2)∵抛物线的对称轴为直线x=1.5,
即点O′在直线x=1.5上,
∴⊙O′与抛物线的第四个交点D与点C关于直线x=1.5对称,如图,
∴D(3,2).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.解决本题的关键是判断△ACB为直角三角形.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
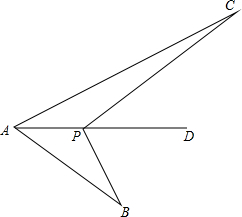 已知点P是∠BAC平分线AD上一点,AC>AB,求证:PC-PB<AC-AB.
已知点P是∠BAC平分线AD上一点,AC>AB,求证:PC-PB<AC-AB.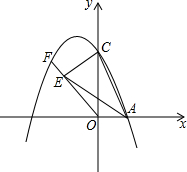 已知抛物线y=-x2+2x+3与x轴正半轴交于A点,与y轴正半轴交于点C,点F在抛物线上,且在第二象限,CE⊥OF于点E,连AC、AE.若AE=AC,求直线OF的解析式.
已知抛物线y=-x2+2x+3与x轴正半轴交于A点,与y轴正半轴交于点C,点F在抛物线上,且在第二象限,CE⊥OF于点E,连AC、AE.若AE=AC,求直线OF的解析式. 看图填空:
看图填空: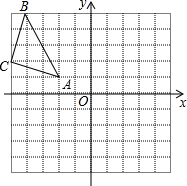 如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).
如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).