题目内容
7.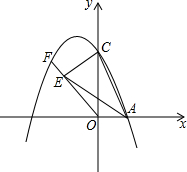 已知抛物线y=-x2+2x+3与x轴正半轴交于A点,与y轴正半轴交于点C,点F在抛物线上,且在第二象限,CE⊥OF于点E,连AC、AE.若AE=AC,求直线OF的解析式.
已知抛物线y=-x2+2x+3与x轴正半轴交于A点,与y轴正半轴交于点C,点F在抛物线上,且在第二象限,CE⊥OF于点E,连AC、AE.若AE=AC,求直线OF的解析式.
分析 由抛物线解析式求出A和C的坐标,由勾股定理得出AE=AC=3$\sqrt{2}$,设直线OF的解析式为y=kx,则直线CE的解析式为y=-kx+3,解方程组$\left\{\begin{array}{l}{y=kx}&{\;}\\{y=-kx+3}&{\;}\end{array}\right.$求出点E的坐标,作EM⊥x轴于M,由勾股定理得出方程,解方程求出k的值即可.
解答 解:∵y=-x2+2x+3,
当y=0时,-x2+2x+3=0,
解得:x=3或x=-1,
∴点A的坐标为(3,0);
当x=0时,y=3,
∴点C的坐标为(0,3),
∴AE=AC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
设直线OF的解析式为y=kx,则直线CE的解析式为y=-kx+3,
解方程组$\left\{\begin{array}{l}{y=kx}&{\;}\\{y=-kx+3}&{\;}\end{array}\right.$得:x=$\frac{3}{2k}$,y=$\frac{3}{2}$,
∴点E坐标为($\frac{3}{2k}$,$\frac{3}{2}$),
作EM⊥x轴于M,如图所示:
由勾股定理得:EM2+AM2=AE2,
即($\frac{3}{2}$)2+($\frac{3}{2k}$-3)2=(3$\sqrt{2}$)2,
解得:k=$\frac{-2-\sqrt{7}}{3}$或k=$\frac{-2+\sqrt{7}}{3}$(舍去),
∴直线OF的解析式为y=$\frac{-2-\sqrt{7}}{3}$x.
点评 本题考查了抛物线与x轴的交点坐标、勾股定理、一次函数解析式的求法等知识;本题有一定难度,需要通过作辅助线运用勾股定理得出方程才能得出结果.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
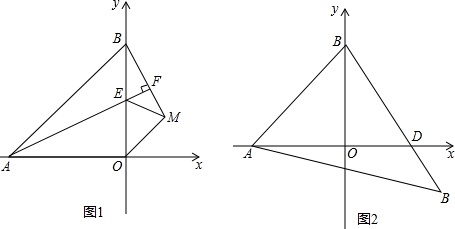
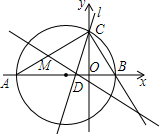 在平面直角坐标系中,△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆与y轴正半轴交于点C,A、B两点的横坐标xA、xB是关于x的方程x2+3x-4=0的两个根.
在平面直角坐标系中,△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆与y轴正半轴交于点C,A、B两点的横坐标xA、xB是关于x的方程x2+3x-4=0的两个根.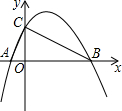 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点,与y轴交与点C,⊙O′为△ABC的外接圆.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点,与y轴交与点C,⊙O′为△ABC的外接圆.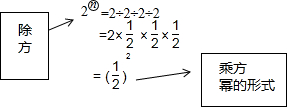 概念学习
概念学习