题目内容
14.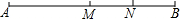 看图填空:
看图填空:(1)MN=AN-AM;
(2)AM=AB-MB;
(3)AB=AM+MN+NB=AM+MB;
(4)若N是MB的中点,M是AB的中点,NB=2,则AN=6.
分析 (1)根据图形填空即可;
(2)根据图形填空即可;
(3)根据图形填空即可;
(4)根据线段中点的性质求出MN、AM,根据AN=AM+MN计算即可.
解答 解:(1)MN=AN-AM;
(2)AM=AB-MB;
(3)AB=AM+MN+NB=AM+MB;
(4)∵N是MB的中点,
∴MN=NB=2,
∵M是AB的中点,
∴AM=MB=4,
∴AN=AM+MN=6.
故答案为:(1)AM;(2)MB;(3)NB;AM;(4)6.
点评 本题考查的是两点间的距离线段中点的性质,灵活运用中点的性质是解题的关键,注意数形结合思想的正确运用.

练习册系列答案
相关题目
3.已知△ABC≌△DEF,∠A=∠D=90°,∠B=43°,则∠E的度数是( )
| A. | 43° | B. | 47° | C. | 47°或43° | D. | 43°或57° |
4.若有理数x,y满足|x|=7,y2=16且|x-y|=y-x,则x+y的值( )
| A. | -11或-3 | B. | -11或3 | C. | 3或11 | D. | -3 |
 正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,求证:以DN、BM、MN为三边的三角形为直角三角形.
正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,求证:以DN、BM、MN为三边的三角形为直角三角形.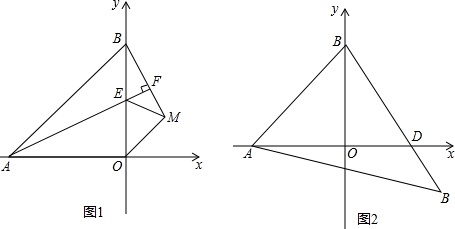
 如图,若线段AC=2,AC=$\frac{1}{5}$AB,点D是线段BC的中点,求线段AD的长度.
如图,若线段AC=2,AC=$\frac{1}{5}$AB,点D是线段BC的中点,求线段AD的长度.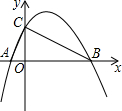 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点,与y轴交与点C,⊙O′为△ABC的外接圆.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点,与y轴交与点C,⊙O′为△ABC的外接圆. 萱萱家为方便她上学,在黄冈小河中学旁边购买了一套经济适用房.她家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
萱萱家为方便她上学,在黄冈小河中学旁边购买了一套经济适用房.她家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题: