题目内容
7.阅读材料:把形如ax2+bx+c的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即a2±2ab+b2=(a±b)2例如:(x-1)2+3、(x-2)2+2x、${({\frac{1}{2}x-2})^2}$+$\frac{3}{4}{x^2}$是x2-2x+4的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项--见横线上的部分).
请根据阅读材料解决下列问题:
(1)比照上面的例子,写出x2-4x+9三种不同形式的配方;
(2)将a2+ab+b2配方(至少两种不同形式);
(3)已知a2+b2+c2-ab-3b-2c+4=0,求a+b+c的值.
分析 (1)(2)根据阅读材料可以得到可以把三项式中的两项作为完全平方式的两项,从而确定第三项即可;
(3)首先分组利用完全平方公式分解因式,利用非负数的性质求得a、b、c的数值,进一步求得a+b+c的值即可.
解答 解:(1)x2-4x+9的三种配方分别为:
x2-4x+9=(x-2)2+5;
x2-4x+9=(x+3)2-10x;
x2-4x+9=(x-3)2+2x(或x2-4x+9=${({\frac{2}{3}x-3})^2}+\frac{5}{9}{x^2}$);
(2)a2+ab+b2=(a+b)2-ab;
或a2+ab+b2=(a+$\frac{1}{2}$b)2+$\frac{3}{4}$b2;
或a2+ab+b2=(a-b)2+3ab;
或a2+ab+b2=(a+b)2-ab;
或a2+ab+b2=${({a+\frac{1}{2}b})^2}+\frac{3}{4}{b^2}$${({\frac{1}{2}a+b})^2}+\frac{3}{4}{a^2}$;
(3)a2+b2+c2-ab-3b-2c+4=0
a2-ab+$\frac{1}{4}$b2+$\frac{3}{4}$(b2-4b+4)+c2-2c+1=0
(a-$\frac{1}{2}$b)2+$\frac{3}{4}$(b-2)2+(c-1)2=0
∴a-$\frac{1}{2}$b=0,$\frac{3}{4}$(b-2)=0,c-1=0
∴a=1,b=2,c=1,
则a+b+c=4.
点评 本题考查了完全平方式,正确读懂题目中的阅读材料,理解配方的方法是关键.另外,注意分组的技巧和方法.

练习册系列答案
相关题目
12.小华问小明:“如图所示的三角形,已知最长边为9,最短边为4,如何求这个三角形的面积?”小明提示说:“可通过作已知一边上的高的方法来解决.”根据小明的提示,小华作出的正确图形是( )
| A. | 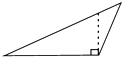 | B. | 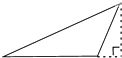 | C. | 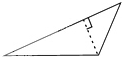 | D. | 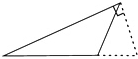 |
16. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,则图中相等的线段共有( )
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,则图中相等的线段共有( )
 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,则图中相等的线段共有( )
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,则图中相等的线段共有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
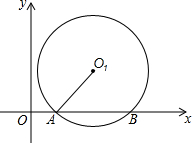 如图,⊙O1与x轴交于A(1,0),B(5,0)两点,⊙O1的半径为3.
如图,⊙O1与x轴交于A(1,0),B(5,0)两点,⊙O1的半径为3.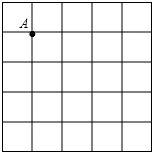 如图,在5×5的正方形网格中,每个小正方形的边长都是1,在所给网格中按下列要求画出图形:
如图,在5×5的正方形网格中,每个小正方形的边长都是1,在所给网格中按下列要求画出图形: