题目内容
10. 如图,已知EF∥CD,∠A=110°,∠EFC=35°,CF为∠ACD的平分线,那么AB与CD平行吗?说明理由.
如图,已知EF∥CD,∠A=110°,∠EFC=35°,CF为∠ACD的平分线,那么AB与CD平行吗?说明理由.
分析 由CF为∠ACD的平分线,根据角平分线的定义可得:∠ACD=2∠FCD,然后由EF∥CD,根据两直线平行内错角相等,可得∠FCD=∠EFC=35°,进而可得:∠ACD=70°,然后根据同旁内角互补两直线平行,即可AB与CD平行.
解答 解:AB与CD平行.
理由如下:
∵CF为∠ACD的平分线,
∴∠ACD=2∠FCD,
∵EF∥CD,
∴∠FCD=∠EFC=35°,
∴∠ACD=70°,
∵∠A+∠ACD=110°+70°=180°,
∴AB∥CD.
点评 此题考查了平行线的判定与性质,解题的关键是:熟记同位角相等?两直线平行,内错角相等?两直线平行,同旁内角互补?两直线平行.

练习册系列答案
相关题目
1.$\sqrt{a+2}$有意义,a的取值范围是( )
| A. | a≥2 | B. | a>2 | C. | a≥-2 | D. | a>-2 |
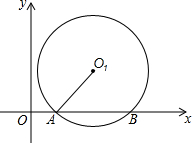 如图,⊙O1与x轴交于A(1,0),B(5,0)两点,⊙O1的半径为3.
如图,⊙O1与x轴交于A(1,0),B(5,0)两点,⊙O1的半径为3.