题目内容
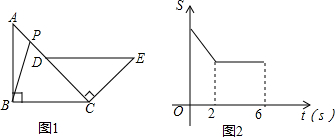
13.在四边形ABCD中,AD=1,AB=7,BC=7,AD∥BC,∠ABC=90°,将线段DC绕点D逆时针转90°到线段DE,求线段AE的长度.(至少用两种方法)分析 方法一:作DH⊥BC于H,EF⊥AD于F,如图1,易得四边形ABHD为矩形,得到BH=AD=1,DH=AB=7,则CH=BC-BH=6,再根据旋转的性质得∠CDE=90°,DC=DE,接着证明△DCH≌△DEF,所以CH=EF=6,DH=DF=7,AF=AD+DF=8,然后在Rt△AEF中利用勾股定理计算AE的长;
方法二:作CH⊥AD于H,EF⊥AD于F,如图2,易得四边形ABCH为矩形,得到AH=BC=7,CH=AB=7,则DH=AH-AD=6,再根据旋转的性质得∠CDE=90°,DC=DE,与方法一一样可证明△DCH≌△EDF得到CH=DF=7,DH=EF=6,AF=AD+DF=8,然后利用勾股定理计算AE的长.
解答 解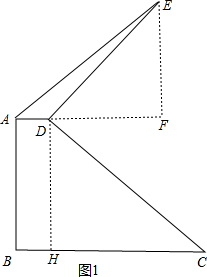 :方法一:作DH⊥BC于H,EF⊥AD于F,如图1,
:方法一:作DH⊥BC于H,EF⊥AD于F,如图1,
∵AD∥BC,∠ABC=90°,
∴四边形ABHD为矩形,
∴BH=AD=1,DH=AB=7,
∴CH=BC-BH=6,
∵线段DC绕点D逆时针转90°到线段DE,
∴∠CDE=90°,DC=DE,
∴∠CDF+∠EDF=90°,
∵∠CDF+∠CDH=90°,
∴∠CDH=∠EDF,
在△DCH和△DEF中
$\left\{\begin{array}{l}{∠DHC=∠DFE}\\{∠CDH=∠EDF}\\{DC=DE}\end{array}\right.$,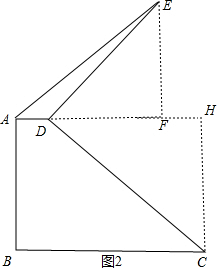
∴△DCH≌△DEF,
∴CH=EF=6,DH=DF=7,
∴AF=AD+DF=8,
在Rt△AEF中,AE=$\sqrt{{6}^{2}+{8}^{2}}$=10;
方法二:作CH⊥AD于H,EF⊥AD于F,如图2,
∵AD∥BC,∠ABC=90°,
∴四边形ABCH为矩形,
∴AH=BC=7,CH=AB=7,
∴DH=AH-AD=6,
∵线段DC绕点D逆时针转90°到线段DE,
∴∠CDE=90°,DC=DE,
与方法一一样可证明△DCH≌△EDF,
∴CH=DF=7,DH=EF=6,
∴AF=AD+DF=8,
在Rt△AEF中,AE=$\sqrt{{6}^{2}+{8}^{2}}$=10.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.本题的关键是构建全等三角形证明线段相等.

 阅读快车系列答案
阅读快车系列答案 如图,在扇形AOB中,∠AOB=90°,弧AB的长为2π,则扇形AOB的面积为4π.
如图,在扇形AOB中,∠AOB=90°,弧AB的长为2π,则扇形AOB的面积为4π.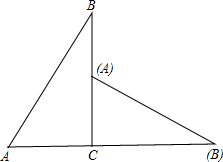 如图,在△ABC中,∠ACB=90°,AB=2BC=2,将△ABC绕点C顺时针旋转得到点B落在边AC上,则边AB在旋转过程中,所扫过的区域面积是$\frac{11}{12}π$+$\frac{\sqrt{3}}{4}$.
如图,在△ABC中,∠ACB=90°,AB=2BC=2,将△ABC绕点C顺时针旋转得到点B落在边AC上,则边AB在旋转过程中,所扫过的区域面积是$\frac{11}{12}π$+$\frac{\sqrt{3}}{4}$.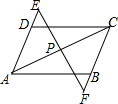 如图,AB=CD,AD=BC,P为AC上任一点,过P的直线分别交AD,CB的延长线于点E,F.
如图,AB=CD,AD=BC,P为AC上任一点,过P的直线分别交AD,CB的延长线于点E,F.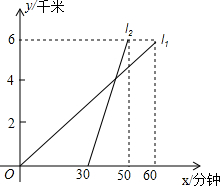 甲乙两车从A地出发,沿同一条公路行驶至距A地6千米的B地,l1、l2分别表示甲乙两车行驶路程y(千米)与时间x(分钟)之间的关系(如图所示).
甲乙两车从A地出发,沿同一条公路行驶至距A地6千米的B地,l1、l2分别表示甲乙两车行驶路程y(千米)与时间x(分钟)之间的关系(如图所示).