题目内容
1.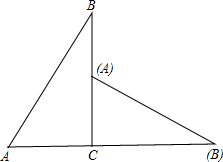 如图,在△ABC中,∠ACB=90°,AB=2BC=2,将△ABC绕点C顺时针旋转得到点B落在边AC上,则边AB在旋转过程中,所扫过的区域面积是$\frac{11}{12}π$+$\frac{\sqrt{3}}{4}$.
如图,在△ABC中,∠ACB=90°,AB=2BC=2,将△ABC绕点C顺时针旋转得到点B落在边AC上,则边AB在旋转过程中,所扫过的区域面积是$\frac{11}{12}π$+$\frac{\sqrt{3}}{4}$.
分析 证明△BCD是等边三角形,得出BD=BC=1,得出AD=BD,求出△ACD的面积,AB所扫过的区域面积=两个扇形的面积+△ACD的面积,即可求得答案.
解答 解:如图所示:
∵∠ACB=90°,AB=2BC=2,
∴∠A=30°,
∴∠B=90°-30°=60°,
又∵BC=CD,
∴△BCD是等边三角形,
∴BD=BC=1,
∴AD=AB-BD=2-1=1,
∴AD=BD,
∴S△ACD=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{4}$,
∴边AB所扫过的图形面积=$\frac{60×π×{1}^{2}}{360}$+$\frac{90×π×(\sqrt{3})^{2}}{360}$+$\frac{\sqrt{3}}{4}$=$\frac{11}{12}π$+$\frac{\sqrt{3}}{4}$.
故答案为:$\frac{11}{12}π$+$\frac{\sqrt{3}}{4}$.
点评 此题考查了旋转的性质、扇形的面积公式、等边三角形的判定与性质、三角形面积的计算等知识.此题有一定难度,根据题意画出图形,得出AB所扫过的图形面积=两个扇形的面积+△ACD的面积是解决问题的关键.

练习册系列答案
相关题目
18.下列说法中,正确的是( )
| A. | 若ac=bc,则a=b | B. | 若$\frac{a}{c}$=$\frac{b}{c}$,则a=b | C. | 若a2=b2,则a=b | D. | 若|a|=|b|,则a=b |
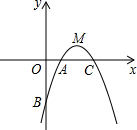 已知二次函数y=-x2+4x-3,其图象与y轴交于点B,与x轴交于A、C 两点,顶点为M.
已知二次函数y=-x2+4x-3,其图象与y轴交于点B,与x轴交于A、C 两点,顶点为M. 如图,△OAB是边长为2的等边三角形,过点A的直线$y=-\frac{\sqrt{3\;}}{3}x$+m与x轴交于点E.
如图,△OAB是边长为2的等边三角形,过点A的直线$y=-\frac{\sqrt{3\;}}{3}x$+m与x轴交于点E.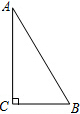 如图,在Rt△ABC中,∠C=90°,∠A=30°.
如图,在Rt△ABC中,∠C=90°,∠A=30°.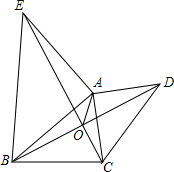 以△ABC的边AB、AC为边向外作等腰直角三角形EAB和等腰直角三角形DAC,∠EAB=∠DAC=90°,EC、BD交于点O.求证:OA平分∠EOD.
以△ABC的边AB、AC为边向外作等腰直角三角形EAB和等腰直角三角形DAC,∠EAB=∠DAC=90°,EC、BD交于点O.求证:OA平分∠EOD.