题目内容
18.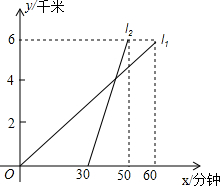 甲乙两车从A地出发,沿同一条公路行驶至距A地6千米的B地,l1、l2分别表示甲乙两车行驶路程y(千米)与时间x(分钟)之间的关系(如图所示).
甲乙两车从A地出发,沿同一条公路行驶至距A地6千米的B地,l1、l2分别表示甲乙两车行驶路程y(千米)与时间x(分钟)之间的关系(如图所示).(1)分别求l1、l2的函数表达式(不要求写出x的取值范围);
(2)甲、乙两车哪一辆先到达B地?这辆快车的行驶速度是多少千米/分钟?
(3)两车在甲出发后多少分钟相遇?
分析 (1)根据函数图象可知l1为正比例函数,过点(60,6)从而可以求得直线l1的表达式,由图象可知l2为一次函数且过点(30,0),(50,6),从而可以求得l2的函数表达式;
(2)由图象可知甲、乙两车哪一辆先到达B地,这辆快车的行驶速度是多少千米/分钟;
(3)将第(1)问中求得函数解析式联立方程组,可以求得两车在甲出发后多少分钟相遇.
解答 解:(1)设l1的解析式为:y=kx
∵点(60,6)在直线l1上,
∴6=60k,
解得k=0.1,
即l1的函数表达式是:y=0.1x;
设l2的函数表达式是:y=mx+n,
∵点(30,0),(50,6),
∴$\left\{\begin{array}{l}{30m+n=0}\\{50m+m=6}\end{array}\right.$
解得m=0.3,n=-9.
即l2的函数表达式是:y=0.3x-9.
(2)由函数图象可知,乙车先到达B地,乙车行驶20分钟走的路程是6千米,
则乙车的速度是6÷20=0.3千米/分钟,
即乙车先到达B地,它的行驶速度是0.3千米/分钟;
(3)$\left\{\begin{array}{l}{y=0.1x}\\{y=0.3x-9}\end{array}\right.$,
解得x=45,y=4.5.
即两车在甲出发后45分钟相遇.
点评 本题考查一次函数的应用,解题的关键是利用数形结合的思想通过函数图象得到所求问题需要的条件.

练习册系列答案
相关题目
 如图,△OAB是边长为2的等边三角形,过点A的直线$y=-\frac{\sqrt{3\;}}{3}x$+m与x轴交于点E.
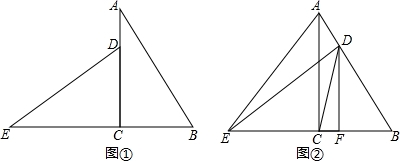
如图,△OAB是边长为2的等边三角形,过点A的直线$y=-\frac{\sqrt{3\;}}{3}x$+m与x轴交于点E.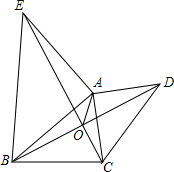 以△ABC的边AB、AC为边向外作等腰直角三角形EAB和等腰直角三角形DAC,∠EAB=∠DAC=90°,EC、BD交于点O.求证:OA平分∠EOD.
以△ABC的边AB、AC为边向外作等腰直角三角形EAB和等腰直角三角形DAC,∠EAB=∠DAC=90°,EC、BD交于点O.求证:OA平分∠EOD. 已知二次函数y=(x+3)2-4的图象与x轴交于点A,B,与y轴交于点c.
已知二次函数y=(x+3)2-4的图象与x轴交于点A,B,与y轴交于点c.