题目内容
2.根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.(1)AB=4cm,BC=6cm,AC=8cm,A′B′=12cm,B′C′=18cm,A′C′=24cm.
(2)∠A=120°,AB=7cm,AC=14cm.∠A′=120°,A′B′=3cm,A′C=6cm.
分析 (1)通过计算得出三边对应成比例,可判定其相似.
(2)∠A=∠A′,再证出$\frac{AB}{A′B′}=\frac{AC}{A′C′}$,即可得出相似.
解答 解:(1)△ABC∽△A′B′C′;理由如下:
∵$\frac{AB}{A′B′}=\frac{4}{12}$=$\frac{1}{3}$,$\frac{BC}{B′C′}=\frac{6}{18}$=$\frac{1}{3}$,$\frac{AC}{A′C′}$=$\frac{8}{24}$=$\frac{1}{3}$,
∴$\frac{AB}{A′B′}=\frac{BC}{B′C′}=\frac{AC}{A′C′}$,
∴△ABC∽△A′B′C′;
(2)△ABC∽△A′B′C′;理由如下:
∵$\frac{AB}{A′B′}=\frac{7}{3}$,$\frac{AC}{A′C′}=\frac{14}{6}=\frac{7}{3}$,
∴$\frac{AB}{A′B′}=\frac{AC}{A′C′}$,
又∵∠A=∠A′=120°,
∴△ABC∽△A′B′C′.
点评 本题主要考查了相似三角形的判定定理;熟练掌握相似三角形的判定定理是解决问题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
17.若x:y=1:3,2y=3z,则$\frac{2x+y}{2x-y}$的值是( )
| A. | -5 | B. | -$\frac{10}{3}$ | C. | $\frac{10}{3}$ | D. | 5 |
14.方程x2=2x的解是( )
| A. | 2 | B. | 0 | C. | 0或2 | D. | 都不是 |
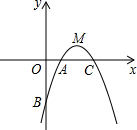 已知二次函数y=-x2+4x-3,其图象与y轴交于点B,与x轴交于A、C 两点,顶点为M.
已知二次函数y=-x2+4x-3,其图象与y轴交于点B,与x轴交于A、C 两点,顶点为M.