题目内容
2.在一个不透明的口袋中,装有A,B,C,D4个完全相同的小球,随机摸取一个小球然后放回,再随机摸取一个小球,两次摸到同一个小球的概率是$\frac{1}{4}$.分析 可以根据画树状图的方法,先画树状图,再求得两次摸到同一个小球的概率.
解答 解:画树状图如下:
∴P(两次摸到同一个小球)=$\frac{4}{16}$=$\frac{1}{4}$
故答案为:$\frac{1}{4}$
点评 本题主要考查了概率,解决问题的关键是掌握树状图法.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列各图形都是轴对称图形,其中对称轴最多的是( )
| A. | 等腰直角三角形 | B. | 直线 | C. | 等边三角形 | D. | 正方形 |
7. 如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )
如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )
 如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )
如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )| A. | 42° | B. | 48° | C. | 52° | D. | 58° |
14. 如图,直线a∥b,c是截线,∠1的度数是( )
如图,直线a∥b,c是截线,∠1的度数是( )
 如图,直线a∥b,c是截线,∠1的度数是( )
如图,直线a∥b,c是截线,∠1的度数是( )| A. | 55° | B. | 75° | C. | 110° | D. | 125° |
4.函数y=$\frac{{a}^{2}+2}{x}$(a为常数)的图象上有三点(-2,y1),(1,y2),(4,y3),则函数值y1、y2、y3的大小关系为( )
| A. | y1<y2<y3 | B. | y2<y3<y${\;}_{{1}_{1}}$ | C. | y1<y3<y2 | D. | y3<y2<y1 |

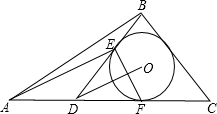 在ABC中,边AC上有一点D满足DC=2AD,O是△BDC的内心,E、F分别为⊙O与边BD、DC的切点,设BD=BC.
在ABC中,边AC上有一点D满足DC=2AD,O是△BDC的内心,E、F分别为⊙O与边BD、DC的切点,设BD=BC.