题目内容
13.已知x=3,y=2,求$\frac{{\sqrt{x}}}{{\sqrt{x}-\sqrt{y}}}-\frac{{\sqrt{y}}}{{\sqrt{x}+\sqrt{y}}}$的值.分析 先通分,再利用平方差公式和二次根式的性质与法则化简,最后计算分式的减法,代入求值即可.
解答 解:原式=$\frac{{\sqrt{x}(\sqrt{x}+\sqrt{y})}}{{(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})}}-\frac{{\sqrt{y}(\sqrt{x}-\sqrt{y})}}{{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}}$
=$\frac{{x+\sqrt{xy}}}{x-y}-\frac{{\sqrt{xy}-y}}{x-y}$
=$\frac{x+y}{x-y}$,
当x=3,y=2时,
原式=$\frac{x+y}{x-y}=\frac{3+2}{3-2}=5$.
点评 本题主要考查分式的化简求值与二次根式的化简求值,熟练掌握分式与二次根式的运算法则与性质是解题的关键.

练习册系列答案
相关题目
5.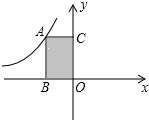 如图,矩形ABOC的面积为$\sqrt{2}$,反比例函数y=$\frac{k}{x}$的图象过点A,则k的值为( )
如图,矩形ABOC的面积为$\sqrt{2}$,反比例函数y=$\frac{k}{x}$的图象过点A,则k的值为( )
 如图,矩形ABOC的面积为$\sqrt{2}$,反比例函数y=$\frac{k}{x}$的图象过点A,则k的值为( )
如图,矩形ABOC的面积为$\sqrt{2}$,反比例函数y=$\frac{k}{x}$的图象过点A,则k的值为( )| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 2 | D. | -2 |
15.平面直角坐标系内,点A(n,n-1)一定不在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如果表示a,b两个数的点在数轴上的位置如图所示,那么化简式子$\sqrt{(a-b)^{2}}$-|a|+$\sqrt{{b}^{2}}$的结果等于( )
如果表示a,b两个数的点在数轴上的位置如图所示,那么化简式子$\sqrt{(a-b)^{2}}$-|a|+$\sqrt{{b}^{2}}$的结果等于( ) 如图,在?ABCD中,AF=CE,求证:AE=CF.
如图,在?ABCD中,AF=CE,求证:AE=CF. 如图,正比例函数y=kx(k≠0)与反比例函数y=-$\frac{2}{x}$的图象交于点A(-1,m)和点B.求点B的坐标.
如图,正比例函数y=kx(k≠0)与反比例函数y=-$\frac{2}{x}$的图象交于点A(-1,m)和点B.求点B的坐标.