题目内容
10.计算:(1)$\sqrt{8}+\sqrt{32}-\sqrt{2}$;
(2)$(\sqrt{2}+\sqrt{3})^{2}-(\sqrt{2}+\sqrt{3})(\sqrt{2}-\sqrt{3})$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)利用完全平方公式和平方差公式计算.
解答 解:(1)原式=2$\sqrt{2}$+4$\sqrt{2}$-$\sqrt{2}$
=5$\sqrt{2}$;
(2)原式=2+2$\sqrt{6}$+3-(2-3)
=5+2$\sqrt{6}$+1
=6+2$\sqrt{6}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.利用乘法公式计算是解决(2)小题的关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
20. 如图,在数轴上表示某不等式组中的两个不等式的解集,那么这个不等式组的解集为( )
如图,在数轴上表示某不等式组中的两个不等式的解集,那么这个不等式组的解集为( )
 如图,在数轴上表示某不等式组中的两个不等式的解集,那么这个不等式组的解集为( )
如图,在数轴上表示某不等式组中的两个不等式的解集,那么这个不等式组的解集为( )| A. | x<-1或x≥2 | B. | x<-1或x>2 | C. | -1≤x<2 | D. | -1<x≤2 |
5.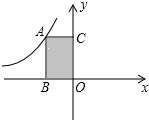 如图,矩形ABOC的面积为$\sqrt{2}$,反比例函数y=$\frac{k}{x}$的图象过点A,则k的值为( )
如图,矩形ABOC的面积为$\sqrt{2}$,反比例函数y=$\frac{k}{x}$的图象过点A,则k的值为( )
 如图,矩形ABOC的面积为$\sqrt{2}$,反比例函数y=$\frac{k}{x}$的图象过点A,则k的值为( )
如图,矩形ABOC的面积为$\sqrt{2}$,反比例函数y=$\frac{k}{x}$的图象过点A,则k的值为( )| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 2 | D. | -2 |
15.互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为200元,按标价的五折销售,仍可获利20元,则这件商品的进价为( )
| A. | 120元 | B. | 100元 | C. | 80元 | D. | 60元 |
19.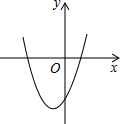 在平面直角坐标系中,二次函数y=x2+2x-3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中-3≤x1<x2≤0,则下列结论正确的是( )
在平面直角坐标系中,二次函数y=x2+2x-3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中-3≤x1<x2≤0,则下列结论正确的是( )
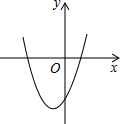 在平面直角坐标系中,二次函数y=x2+2x-3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中-3≤x1<x2≤0,则下列结论正确的是( )
在平面直角坐标系中,二次函数y=x2+2x-3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中-3≤x1<x2≤0,则下列结论正确的是( )| A. | y1<y2 | B. | y1>y2 | C. | y的最小值是-3 | D. | y的最小值是-4 |
 如图,正比例函数y=kx(k≠0)与反比例函数y=-$\frac{2}{x}$的图象交于点A(-1,m)和点B.求点B的坐标.
如图,正比例函数y=kx(k≠0)与反比例函数y=-$\frac{2}{x}$的图象交于点A(-1,m)和点B.求点B的坐标.