题目内容

5．如图，有一个边长为20cm的正方形洞口，想用一个圆盖去盖住这个洞口，则圆盖的直径（结果保留整数）至少是（　　）
A．20cmB．28cmC．29cmD．40cm

分析 根据圆形盖的直径最小应等于正方形的对角线的长，才能将洞口盖住，根据勾股定理进行解答．

解答 解：∵正方形的边长为20cm，
∴正方形的对角线长为$\sqrt{2{0}^{2}+2{0}^{2}}$=20$\sqrt{2}$≈28.28（cm），
∴想用一个圆盖去盖住这个洞口，则圆盖的直径（结果保留整数）至少是29cm；
故选：C．

点评 本题考查的是正多边形和圆、勾股定理的应用，根据正方形和圆的关系确定圆的直径是解题的关键．

练习册系列答案
相关题目
7．x的4倍与7的差不小于-1，可列关系式为（　　）
A．4x-7≤-1B．4x-7＜-1C．4x-7=-1D．4x-7≥-1
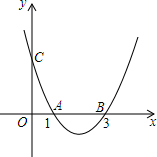8．（1）已知二次函数y=（x-1）（x-3）的图象如图，请根据图象直接写出该二次函数图象经过怎样的左右平移，新图象通过坐标原点？
（2）在关于二次函数图象的研究中，秦篆晔同学发现抛物线y=ax2-bx+c（a≠0）和抛物线y=ax2-bx+c（a≠0）关于y轴对称，基于协作共享，秦同学将其发现口诀化“a、c不变，b相反”供大家分享，而在旁边补笔记的胡庄韵同学听成了“a、c相反，b不变”，并按此法误写，然而按此误写的抛物线恰巧与原抛物线也对称，请你写出小胡同学所写的与原抛物y=（x-1）（x-3）的对称图形的解析式，并研究其与原抛物线的具体对称情况；
（3）抛物线y=（x-1）（x-3）与x轴从左到右交于A、B两点，与y轴交于点C，M是其对称轴上一点，点N在x轴上，当点N满足怎样的条件，以点N、B、C为顶点的三角形与△MAB有可能相似，请写出所有满足条件的点N的坐标；
（4）E、F为抛物线y=（x-1）（x-3）上两点，且E、F关于D（$\frac{3}{2}$，0）对称，请直接写出E、F两点的坐标．
13．如图，在平面直角坐标系内，直线AB过一、二、三象限，分别交x轴、y轴于A、B两点，直线CD⊥AB于点D，分别交x轴、y轴于C、E，已知AB=AC=10，S△ACD=8，且B（0，6）．
（1）求证：△AOB≌△ADC；
（2）求点A的坐标；
（3）点M为线段OA上一动点，作∠NME=∠OME，且MN交AD于点N，当点M运动时，求$\frac{MO+ND}{MN}$的值．
20．如图，在直角坐标系xOy中，Rt△AOB的两直角边分别在两坐标轴上，A（a，0），B（0，a），OC⊥AB于C．
（1）若a=8，求△AOC的面积；
（2）直线AD分别交OC于D，交y轴于E，且OD=OE，过B作BF⊥直线AD于F，求证：AE=2BF；
（3）点G与B关于x轴对称，点P是X轴负半轴上一动点，过点P作BP的垂线与AG相交于点H，若点M为第一象限内任一点，过点B作BQ⊥HM于Q，当点P在x轴的负半轴上运动时，∠BQP的度数是否发生变化？若不变，请求出∠BQP的度数；若变化，请求出其变化范围．
10．把下面的说理过程补充完整．
已知：如图，∠1+∠2=180°，∠3=∠B，试判断∠AED与∠C的关系，并说明理由．
解：∠AED=∠C
∵∠1+∠ADG=180°（平角定义），∠1+∠2=180°（已知）
∴∠2=∠ADG（同角的补角相等）
∴EF∥AB（同位角相等，两直线平行）
∴∠3=∠ADE（两直线平行，内错角相等 ）
∵∠3=∠B（已知）∴∠B=∠ADE  （等量代换）
∴DE∥BC（同位角相等，两直线平行）
∴∠AED=∠C（两直线平行，同位角相等 ）
17．如图，OP平分∠AOB，PD⊥OA于点D，点Q是射线OB上一个动点，若PD=2，则PQ的最小值为（　　）
A．PQ＜2B．PQ=2
C．PQ＞2D．以上情况都有可能
14．如图，点P是菱形ABCD的对角线BD上一点，连接CP，延长后交AD于点E，交BA的延长线于点F．
（1）求证：△APD≌△CPD；
（2）求证：PC2=PE•PF；
（3）若PE=2，EF=6，FB=16，求菱形ABCD的边长．
15．（1）先化简，再求值$\frac{1}{2}x-2（{x-\frac{1}{3}{y^2}}）+（{-\frac{3}{2}x+\frac{1}{3}{y^2}}）$，其中x，y满足|x-2|+（y+1）2=0
（2）已知一个角的余角比这个角的4倍少10°，求这个角的补角的度数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网