题目内容
3.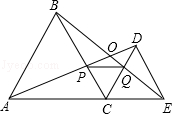 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下三个结论:①AD=BE;②EQ=DP;③△CPQ是等边三角形;其中一定成立的结论有①②③.
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下三个结论:①AD=BE;②EQ=DP;③△CPQ是等边三角形;其中一定成立的结论有①②③.
分析 根据等边三角形性质得出AB=BC=AC,DC=CE=DE,∠BCA=∠DCE=∠EDC=∠DEC=60°,推出∠ACD=∠BCE,根据SAS证△ACD≌△BCE,即可推出①;根据ASA证△DPC≌△EQC,推出CP=CQ,证三角形CPQ是等边三角形,即可推出②;
解答 解:
∵等边△ABC和等边△DCE,
∴BC=AC,DE=DC=CE,∠DEC=∠BCA=∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{DC=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠CBE=∠DAC,AD=BE,∴①正确;
∵△ACD≌△BCE,
∴∠ADC=∠BEC,
在△DPC和△EQC中
$\left\{\begin{array}{l}{∠CDA=∠CEB}\\{CD=CE}\\{∠DCP=∠ECD}\end{array}\right.$,
∴△DPC≌△EQC(ASA),
∴EQ=DP,故②正确;
CP=CQ,
∵∠BCD=60°,
∴△CPQ是等边三角形,故③正确,
综上可知正确的结论①②③,
故答案为:①②③.
点评 本题主要考查等边三角形的性质及全等三角形的判定等知识点,得到三角形全等是正确解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.如图图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第10个图案中白色正方形的个数为( )
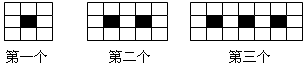

| A. | 50 | B. | 53 | C. | 55 | D. | 60 |
1.下列说法不正确的是( )
| A. | 有限小数和无限循环小数都能化成分数 | |
| B. | 整数可以看成是分母为1的分数 | |
| C. | 有理数都可以化为分数 | |
| D. | 无理数是无限循环的数 |