题目内容
6．下列各数：$\frac{1}{7}$，-π，-$\sqrt{3}$，0.$\stackrel{•}{3}$，-0.1010010001…（两个1之间依次多一个0），-$\sqrt{49}$中无理数的个数为（ ）| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
分析 无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
解答 解：-π，-$\sqrt{3}$，-0.1010010001…（两个1之间依次多一个0）是无理数，
故选：B．
点评 此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知∠1=∠2，AC=AD，有下列条件：①AB=AE；②BC=ED；③∠C=∠D；④∠B=∠E．其中能使△ABC∽△AED的条件有 （ ）
17．在下列长度的四根木棒中，能与4cm、9cm长的两根木棒钉成一个三角形的是（ ）
| A． | 4cm | B． | 5cm | C． | 7cm | D． | 14cm |
1．
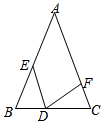如图，在△ABC中，AB=AC，BD=CF，BE=CD，若∠A=40°，则∠EDF的度数为（ ）
如图，在△ABC中，AB=AC，BD=CF，BE=CD，若∠A=40°，则∠EDF的度数为（ ）| A． | 75° | B． | 70° | C． | 65° | D． | 60° |
4．下列运算中，正确的是（ ）
| A． | x•x3=x3 | B． | （x2）3=x5 | C． | x6÷x2=x4 | D． | （x-y）2=x2-y2 |