题目内容
20．若直线y=3x+m经过第一、三、四象限，则抛物线y=（x-m）2+1的顶点在第（ ）象限．| A． | 一 | B． | 二 | C． | 三 | D． | 四 |
分析 由直线y=3x+m经过第一，三，四象限可判断m的符号，再由抛物线y=（x-m）2+1求顶点坐标，判断象限．
解答 解：∵直线y=3x+m经过第一，三，四象限，
∴m＜0，
∴抛物线y=（x-m）2+1的顶点（m，1）必在第二象限．
故选B．
点评 本题考查了一次函数图象与系数的关系、二次函数图象与系数的关系，掌握直线性质和抛物线顶点式是解题的关键．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
10．小涵将如图1所示学习桌的桌面抽象成了如图2所示的多边形，则图2中∠A+∠B+∠C+∠D+∠E+∠F等于（ ）
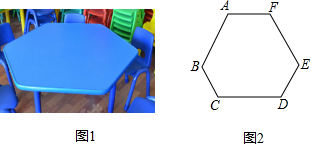
| A． | 640° | B． | 1080° | C． | 900° | D． | 720° |
11．
如图是一个少数民族手鼓的轮廓图，其主视图是（ ）
如图是一个少数民族手鼓的轮廓图，其主视图是（ ）| A． |  | B． |  | C． |  | D． |  |
8．下列各数$0.\stackrel{•}{3}$，5π，$\root{3}{64}$，-0.125，$\sqrt{0.2}$，$\frac{\sqrt{3}}{2}$，$\frac{23}{7}$中，无理数的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
15．对于多项式x2-2x-18，下列说法中正确的是（ ）
| A． | 它是二次三项式 | B． | 它的常数项是18 | ||
| C． | 它的一次项系数是-2x | D． | 它的二次系数是0 |
5．已知x=2是一元二次方程x2+mx+2=0的一个解，则m的值是（ ）
| A． | -3 | B． | 3 | C． | 0 | D． | 0或3 |
12．下列各数中，最小的数是（ ）
| A． | -1 | B． | -$\frac{1}{3}$ | C． | 0 | D． | 1 |
10．下列轴对称图形中，对称轴的数量小于3的是（ ）
| A． |  | B． |  | C． |  | D． |  |