题目内容
3. 如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠BAO.
如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠BAO.
分析 由菱形的性质得出OD=OB,AC⊥BD,由直角三角形斜边上的中线等于斜边的一半得出OH=$\frac{1}{2}$BD=OB,得出∠OHB=∠OBH,再由∠BAO+∠OBA=90°,∠DHO+∠OHB=90°,
即可得出∠DHO=∠BAO.
解答 证明:∵四边形ABCD是菱形,
∴OD=OB,AC⊥BD,
∵DH⊥AB于H,
∴∠DHB=90°,
∴OH=$\frac{1}{2}$BD=OB,
∴∠OHB=∠OBH,
在Rt△AOB中,∠BAO+∠OBA=90°,
在Rt△DHB中,∠DHO+∠OHB=90°,
∴∠DHO=∠BAO.
点评 本题考查了菱形的性质、直角三角形斜边上的中线性质、等腰三角形的判定与性质,角的互余关系;熟练掌握菱形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.若10y=5,则102-2y等于( )
| A. | 75 | B. | 4 | C. | -5或5 | D. | $\frac{4}{5}$ |
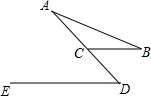 如图已知,BC∥DE,∠A=26°,∠B=34°,求∠D的度数.
如图已知,BC∥DE,∠A=26°,∠B=34°,求∠D的度数.