题目内容
10．当-1＜x＜2时，化简$\sqrt{{x}^{2}+2x+1}$+$\sqrt{{x}^{2}-6x+9}$=4．分析 首先把根号里的式子写成完全平方式，然后根据条件进行化简．
解答 解：当-1＜x＜2时，$\sqrt{{x}^{2}+2x+1}$+$\sqrt{{x}^{2}-6x+9}$=$\sqrt{（x+1）^{2}}+\sqrt{（（x-3）^{2}}$
=x+1+3-x=4．
故答案为4．
点评 本题主要考查了二次根式的性质和化简的知识点，熟练掌握二次根式的性质是解答本题的关键，本题难度不大．
练习册系列答案
名校课堂系列答案
相关题目
已知AB∥CD，图中∠A、∠C、∠P有怎样的数量关系？用式子表示并说明理由．
如图，在平面直角坐标系中，顶点为（2，-1）的抛物线交y轴于A点，交x轴于B、C两点（点B在点C的左侧），已知A点坐标为（0，3），连接AB．
5．下列说法：
①若a与c相交，则a与b相交；
②若a∥b，b∥c，那么a∥c；
③过一点有且只有一条直线与已知直线平行；
④在同一平面内，两条直线的位置关系有平行、相交、垂直三种．
其中错误的有（ ）
①若a与c相交，则a与b相交；
②若a∥b，b∥c，那么a∥c；
③过一点有且只有一条直线与已知直线平行；
④在同一平面内，两条直线的位置关系有平行、相交、垂直三种．
其中错误的有（ ）
| A． | 3个 | B． | 2个 | C． | 1个 | D． | 0个 |
如图所示，A、B之间是一座山，一条铁路要通过A、B两地，在A地测得铁路走向是北偏东48°25′，则在B地测得A地在南偏西多少度？如果A、B两地同时开工，那么在B地按∠β施工，∠β为多少度才能使铁路在山腹中准确接通？
2．下列式子中，正确的是（ ）
| A． | x3•x5=x15 | B． | （-x3）2=x9 | C． | （3x2y）2=3x4y | D． | （-2x2y）2=4x4y2 |
如图，在?ABCD中，DE平分∠ADC交AB于点G，交CB延长线于E，BF平分∠ABC交AD的延长线于F．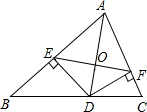
如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高，则下列结论：