题目内容
18.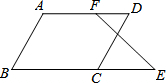 已知:如图,AB∥CD.∠A+∠DCE=180°,求证:∠E=∠DFE.
已知:如图,AB∥CD.∠A+∠DCE=180°,求证:∠E=∠DFE.证明:∵AB∥CD ( 已知 ),
∴∠B=∠DCE(两直线平行,同位角相等).
∵∠A+∠DCE=180°(已知),
∴∠E=∠DFE(两直线平行,内错角相等).
分析 由平行线的性质得出同位角相等,再由已知条件得出AD∥BC,即可得出结论.
解答 解:∵AB∥CD ( 已知 ),
∴∠B=∠DCE( 两直线平行,同位角相等).
∵∠A+∠DCE=180°(已知),
∴∠A+∠B=180°,
∴AD∥BC(同旁内角互补,两直线平行),
∴∠E=∠DFE(两直线平行,内错角相等).
故答案为:DCE;两直线平行,同位角相等.
点评 本题考查了平行线的性质与判定;熟练掌握平行线的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
9.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a2-b2=(a-b)2 | C. | (3b3)2=6b6 | D. | (-a)5÷(-a)3=a2 |
6.在Rt△ABC中,∠C=90°,下列式子中不一定成立的是( )
| A. | cosA=sinB | B. | sinA=cosB | C. | sin(A+B)=sinC | D. | sinA=sinB |
 有理数a,b,c在数轴上的相应位置如图所示,化简|a|+|b|-|c|.
有理数a,b,c在数轴上的相应位置如图所示,化简|a|+|b|-|c|.